Termodinamika példák - Nyomás hőmérsékletfüggése mérhető mennyiségekkel
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Stippinger (vitalap | szerkesztései) 2013. április 28., 18:02-kor történt szerkesztése után volt.
Feladat
- A
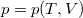 állapotegyenlet ismeretében fejezzük ki a
állapotegyenlet ismeretében fejezzük ki a 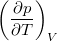 mennyiséget a
mennyiséget a 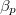 hőtágulási együttható és a
hőtágulási együttható és a 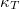 izotermikus kompresszibilitás segítségével!
izotermikus kompresszibilitás segítségével!
Megoldás
Az izobár hőtágulási együttható és az izoterm kompresszibilitás rendre
![\[ \beta_p = \frac 1 V{\left(\frac{\partial V}{\partial T}\right)}_ p, \qquad \kappa_T = -\frac 1 V{\left(\frac{\partial V}{\partial p}\right)}_ T.\]](/images/math/3/3/e/33e0f367042e48ed1e1fba064ff1dc56.png)
Izobár folyamatban
![\[ \mathrm{d}p = 0 = \left(\frac{\partial p}{\partial T}\right)_V \,\mathrm{d}T + \left(\frac{\partial p}{\partial V}\right)_T \,\mathrm{d}V, \]](/images/math/9/b/b/9bbcd1fae54dc65c9e7047808eb8348c.png)
és a 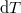 -vel való formális osztás során jelölnünk kell az izobár állapotváltozást:
-vel való formális osztás során jelölnünk kell az izobár állapotváltozást:
![\[ {\left(\frac{\partial p}{\partial T}\right)}_V = -{\left(\frac{\partial p}{\partial V}\right)}_T {\left(\frac{\partial V}{\partial T}\right)}_p = \frac 1{V\kappa_T}\cdot V\beta_p = \frac{\beta_p}{\kappa_ T}. \]](/images/math/4/a/6/4a61605d6b2db0de49b54b971efb0777.png)
Megjegyzés
Gyorsabban juthatunk el az eredményhez izochor folyamattal:
![\[ \mathrm{d}V = 0 = \left(\frac{\partial V}{\partial T}\right)_p \,\mathrm{d}T + \left(\frac{\partial V}{\partial p}\right)_T \,\mathrm{d}p = V\beta_p \,\mathrm{d}T - V\kappa_T \,\mathrm{d}p, \]](/images/math/8/2/6/82613885efcb3b7605484717efd6370a.png)
formálisan osztunk 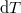 -vel, és jelöljük kell az izochor állapotváltozást:
-vel, és jelöljük kell az izochor állapotváltozást:
![\[ {\left(\frac{\partial p}{\partial T}\right)}_V = \frac{\beta_p}{\kappa_T}. \]](/images/math/c/4/f/c4fcbf429061d44dfada22dc0e50cdfe.png)