„Termodinamika példák - Szilárd-folyadék átalakulás közelítő egyensúlyi görbéje” változatai közötti eltérés
A Fizipedia wikiből
a (Szöveg koherenssé tétele.) |
|||
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># A szilárd-folyadék egyensúlyi | + | </noinclude><wlatex># A szilárd-folyadék egyensúlyi görbének (olvadási görbe) közelítő meghatározására gyakran használják a $\displaystyle p= p_1+\frac{L_M^{\text{olv}}}{\Delta V_M^{\text{olv}}}\ln \frac T{T_1}$ összefüggést ($T_1$ a $p_1$ nyomáson, $T$ a $p$ nyomáson érvényes olvadáspont, az egyenletben szereplő $L_M^{\text{olv}}$ az anyag moláris átalakulási hője (vagy moláris entalpiaváltozása), $\Delta V_M^{\text{olv}}$ pedig a móltérfogat változása az olvadásnál).</wlatex> |
| − | #* a) <wlatex>Vezessük le ezt az egyenletet, és állapítsuk meg, hogy milyen feltételek mellett érvényes!</wlatex><includeonly><wlatex>{{Útmutatás|content= | + | #* a) <wlatex>Vezessük le ezt az egyenletet, és állapítsuk meg, hogy milyen feltételek mellett érvényes!</wlatex><includeonly><wlatex>{{Útmutatás|content=Integráljuk a Clausius-Clapeyron-egyenletet!}}</wlatex></includeonly> |
| − | #* b) <wlatex>Mutassuk ki, hogy a $T_1$-hez képest kis $T-T_1$ érték eseten az egyensúlyi nyomás lineárisan változik a $T-T_1$ különbséggel!</wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk fel a kis | + | #* b) <wlatex>Mutassuk ki, hogy a $T_1$-hez képest kis $T-T_1$ érték eseten az egyensúlyi nyomás lineárisan változik a $T-T_1$ különbséggel!</wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk fel a kis $x$-ekre érvényes $\ln \left(1+x\right)\approx x$ összefüggést.}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>'''a)''' Két | + | <wlatex>'''a)''' Két fázis egyensúlyának szükséges feltétele, hogy |
$$ p_1 = p_2 = p, $$ | $$ p_1 = p_2 = p, $$ | ||
$$ T_1 = T_2 = T, $$ | $$ T_1 = T_2 = T, $$ | ||
| 22. sor: | 23. sor: | ||
azaz a teljes differenciálok megegyeznek: | azaz a teljes differenciálok megegyeznek: | ||
$$ \left(\frac{\partial \mu_1}{\partial p}\right)_T\,\mathrm{d}p + \left(\frac{\partial \mu_1}{\partial T}\right)_p\,\mathrm{d}T | $$ \left(\frac{\partial \mu_1}{\partial p}\right)_T\,\mathrm{d}p + \left(\frac{\partial \mu_1}{\partial T}\right)_p\,\mathrm{d}T | ||
| − | = \left(\frac{\partial \mu_2}{\partial p}\right)_T\,\mathrm{d}p + \left(\frac{\partial \mu_2}{\partial T}\right)_p\,\mathrm{d}T $$ | + | = \left(\frac{\partial \mu_2}{\partial p}\right)_T\,\mathrm{d}p + \left(\frac{\partial \mu_2}{\partial T}\right)_p\,\mathrm{d}T. $$ |
| − | A kémiai potenciálra | + | A kémiai potenciálra érvényes [[Termodinamika példák - A termodinamika differenciális összefüggései|differenciális összefüggéseket]] behelyettesítve: |
$$ \left(S_{M2}-S_{M1}\right)\,\mathrm{d}T = \left(V_{M2}-V_{M1}\right)\,\mathrm{d}p. $$ | $$ \left(S_{M2}-S_{M1}\right)\,\mathrm{d}T = \left(V_{M2}-V_{M1}\right)\,\mathrm{d}p. $$ | ||
| − | A Clausius-Clapeyron egyenlet: | + | A ''Clausius''-''Clapeyron'' egyenlet: |
$$ \frac{\mathrm{d}p}{\mathrm{d}T} = \frac{S_{M2}-S_{M1}}{V_{M2}-V_{M1}}. $$ | $$ \frac{\mathrm{d}p}{\mathrm{d}T} = \frac{S_{M2}-S_{M1}}{V_{M2}-V_{M1}}. $$ | ||
| − | Az átalakulás állandó $T$ hőmérsékleten megy végbe, így az entrópiaváltozás egyszerűen kifejezhető a redukált hővel, a Clapeyron-egyenletet nyerjük: | + | Az átalakulás állandó $T$ hőmérsékleten megy végbe, így az entrópiaváltozás egyszerűen kifejezhető a redukált hővel, a ''Clapeyron''-egyenletet nyerjük: |
$$ \frac{\mathrm{d}p}{\mathrm{d}T} = \frac{L_M}{T\Delta V_M}. $$ | $$ \frac{\mathrm{d}p}{\mathrm{d}T} = \frac{L_M}{T\Delta V_M}. $$ | ||
| − | + | Ezt változószétválasztás után $p$ és $T$ szerint kiintegrálva szilárd-folyadék fázisátmenetre, feltéve, hogy $ L_M^\text{olv}$ és $\Delta V_M^\text{olv}$ sem függ a hőmérséklettől: | |
$$ p = p_1+\frac{L_M^\text{olv}}{\Delta V_M^\text{olv}}\ln \frac T{T_1}. $$ | $$ p = p_1+\frac{L_M^\text{olv}}{\Delta V_M^\text{olv}}\ln \frac T{T_1}. $$ | ||
A lap 2013. május 28., 21:57-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fázisátalakulások |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- A szilárd-folyadék egyensúlyi görbének (olvadási görbe) közelítő meghatározására gyakran használják a
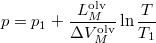összefüggést (
a 
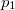nyomáson, 
a 
nyomáson érvényes olvadáspont, az egyenletben szereplő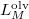 
az anyag moláris átalakulási hője (vagy moláris entalpiaváltozása), 
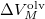pedig a móltérfogat változása az olvadásnál).
- a) Vezessük le ezt az egyenletet, és állapítsuk meg, hogy milyen feltételek mellett érvényes!
- b) Mutassuk ki, hogy a -hez képest kis
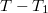érték eseten az egyensúlyi nyomás lineárisan változik a 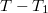különbséggel!
Megoldás
a) Két fázis egyensúlyának szükséges feltétele, hogy
![\[ p_1 = p_2 = p, \]](/images/math/6/d/c/6dc0fe3fae653683a9832e008feb0241.png)
![\[ T_1 = T_2 = T, \]](/images/math/9/8/d/98d08f065366eff6110174c21464017c.png)
![\[ \mu_1\left(p,T\right) = \mu_2\left(p,T\right) \]](/images/math/0/0/6/0060fa339b7a4fc280142bc88fd854e1.png)
A harmadik feltételből adódik, hogy az egyensúlyi görbén elmozdulva
![\[ \mathrm{d}\mu_1 = \mathrm{d}\mu_2, \]](/images/math/6/5/f/65fac2c55da9c4655d447c04f62bce42.png)
azaz a teljes differenciálok megegyeznek:
![\[ \left(\frac{\partial \mu_1}{\partial p}\right)_T\,\mathrm{d}p + \left(\frac{\partial \mu_1}{\partial T}\right)_p\,\mathrm{d}T = \left(\frac{\partial \mu_2}{\partial p}\right)_T\,\mathrm{d}p + \left(\frac{\partial \mu_2}{\partial T}\right)_p\,\mathrm{d}T. \]](/images/math/1/9/3/193df0f3ca0f2672a2017c131687be5a.png)
A kémiai potenciálra érvényes differenciális összefüggéseket behelyettesítve:
![\[ \left(S_{M2}-S_{M1}\right)\,\mathrm{d}T = \left(V_{M2}-V_{M1}\right)\,\mathrm{d}p. \]](/images/math/3/8/f/38f99111c080a03d4faf6c5b3cf31785.png)
A Clausius-Clapeyron egyenlet:
![\[ \frac{\mathrm{d}p}{\mathrm{d}T} = \frac{S_{M2}-S_{M1}}{V_{M2}-V_{M1}}. \]](/images/math/1/9/e/19ea55d898cff4c7435cb2d3ac4a7b27.png)
Az átalakulás állandó hőmérsékleten megy végbe, így az entrópiaváltozás egyszerűen kifejezhető a redukált hővel, a Clapeyron-egyenletet nyerjük:
![\[ \frac{\mathrm{d}p}{\mathrm{d}T} = \frac{L_M}{T\Delta V_M}. \]](/images/math/a/0/f/a0fec1a8cfebf50be3236f388d120097.png)
Ezt változószétválasztás után és szerint kiintegrálva szilárd-folyadék fázisátmenetre, feltéve, hogy 
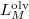és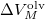 
sem függ a hőmérséklettől:
![\[ p = p_1+\frac{L_M^\text{olv}}{\Delta V_M^\text{olv}}\ln \frac T{T_1}. \]](/images/math/7/4/8/7484dbbd27794b9374fe617c8756df48.png)
b) Ha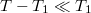 
, alkalmazhatjuk 
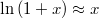közelítést:
![\[ p = p_1+\frac{L_M^\text{olv}}{\Delta V_M^\text{olv}}\ln \frac{T-T_1+T_1}{T_1} = p_1+\frac{L_M^\text{olv}}{\Delta V_M^\text{olv}}\ln \left(1+\frac{T-T_1}{T_1}\right) \approx p_1+\frac{L_M^\text{olv}}{\Delta V_M^\text{olv}}\frac{T-T_1}{T_1}. \]](/images/math/0/1/f/01fdae02453d8dcc60eddb638ca79aea.png)
