Magnetosztatika - Biot-Savart törvény, gerjesztési törvény
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Csorean (vitalap | szerkesztései) 2021. március 23., 18:55-kor történt szerkesztése után volt.
Feladatok
- Határozzuk meg egy
 áram által átjárt véges hosszúságú egyenes vezető mágneses terét a vezetőtől
áram által átjárt véges hosszúságú egyenes vezető mágneses terét a vezetőtől  távolságra található az
távolságra található az  pontban. A vezető szakasz egyik vége
pontban. A vezető szakasz egyik vége  pontból
pontból 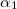 , míg a másik vége
, míg a másik vége 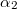 szög alatt látszódik az
szög alatt látszódik az  -ból a vezetőre állított merőlegeshez képest.
-ból a vezetőre állított merőlegeshez képest.
- Határozzuk meg egy végtelen hosszú egyenes vezető mágneses terét, mint a vezetőtől mért távolság függvényét! A vezetőben
 áram folyik. A számításokat végezzük az Amper-féle gerjesztési törvény segítségével!
áram folyik. A számításokat végezzük az Amper-féle gerjesztési törvény segítségével!
- Határozzuk meg a mágneses indukciót az ábra alapján megadott
 áram által átjárt vezető elrendezés
áram által átjárt vezető elrendezés  pontjában!(ábra)
pontjában!(ábra)
 sugarú hengeres vezetékben az áramsűrűség
sugarú hengeres vezetékben az áramsűrűség 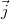 vektora mindenütt azonos és párhuzamos a henger tengelyével. A tengelyre merőleges
vektora mindenütt azonos és párhuzamos a henger tengelyével. A tengelyre merőleges 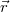 vektor segítségével fejezzük ki a
vektor segítségével fejezzük ki a 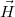 térerősséget az
térerősséget az 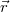 -el jelzett pontban
-el jelzett pontban
a) a hengeren belül;
b) és kívül.
- Tömör fémből készült, hosszú, egyenes körhengerben ugyancsak henger alakú üreget készítünk. Az üreg tengelye
 távolságra van a henger tengelyétől. Az üreges hengerben egyenletes
távolságra van a henger tengelyétől. Az üreges hengerben egyenletes  áramsűrűséggel tengelyirányú áram folyik. Milyen a mágneses térerősség az üreg belsejében?
áramsűrűséggel tengelyirányú áram folyik. Milyen a mágneses térerősség az üreg belsejében?
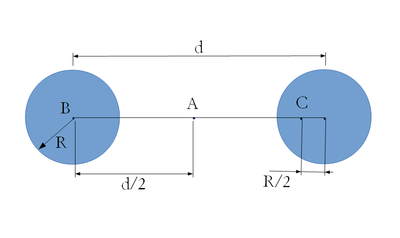
- Két egymással párhuzamos, végtelen hosszú
 sugarú hengeres vezetőben
sugarú hengeres vezetőben  erősségű áram folyik azonos irányban, az ábra síkjára merőlegesen befelé. A hengerek tengelytávolsága
erősségű áram folyik azonos irányban, az ábra síkjára merőlegesen befelé. A hengerek tengelytávolsága  . Az áramsűrűség a vezetők keresztmetszetén állandó. Mekkora a
. Az áramsűrűség a vezetők keresztmetszetén állandó. Mekkora a  mágneses indukció az ábrán jelölt
mágneses indukció az ábrán jelölt  ,
,  ,
,  és pontokban?
és pontokban?
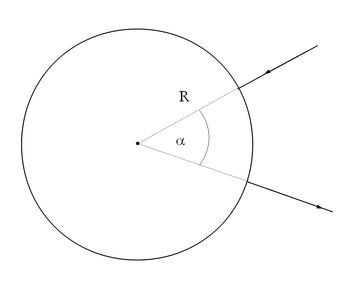
- Az ábra szerinti áramkör egy homogén vezető gyűrűből áll, amelyhez két sugárirányú vezeték csatlakozik. Az áramkört záró forrás a hozzávezetésekkel együtt olyan távoli, hogy a gyűrű helyén keltett mágneses tere elhanyagolható. Mekkora a mágneses térerősség a gyűrű középpontjában?
- Egy
 oldalú négyzet alakú fémkeretben
oldalú négyzet alakú fémkeretben  áram folyik. Határozzuk meg a mágneses térerősséget a keret középpontján átmenő, síkjára merőleges
áram folyik. Határozzuk meg a mágneses térerősséget a keret középpontján átmenő, síkjára merőleges  tengely mentén!
tengely mentén!
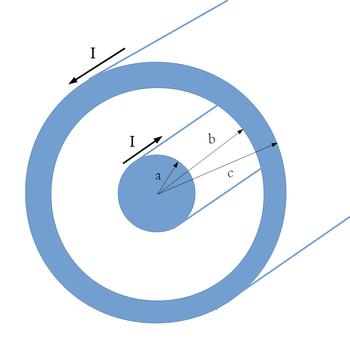
- Az ábrán látható koaxiális vezetőben
 áram folyik. A belső éren (
áram folyik. A belső éren ( -n belül) befelé, a külső éren (
-n belül) befelé, a külső éren ( és
és  között) kifelé. Határozzuk meg a mágneses teret a tengelytől mért
között) kifelé. Határozzuk meg a mágneses teret a tengelytől mért  távolság függvényében.
távolság függvényében.
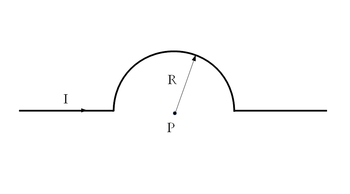
- Az ábrán látható vezető körben
 áram folyik.
áram folyik.
a) Mekkora és milyen irányú az sugarú kör középpontjában a mágneses térerősségnek a körvezetőtől származó része, ha az
sugarú kör középpontjában a mágneses térerősségnek a körvezetőtől származó része, ha az  és
és  pontokat összekötő negyedkörív alakú vezető keresztmetszete
pontokat összekötő negyedkörív alakú vezető keresztmetszete 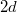 átmérőjű, míg a háromnegyed körívé
átmérőjű, míg a háromnegyed körívé  ?
?
b) Mekkora és milyen irányú mágneses teret kelt a körhöz csatlakozó két vezető szakasz?
c) Mekkora és milyen irányú teret kelt a másik két egyenes vezető szakasz, ha ezeknek a szakaszoknak a hossza ?
?
d) Mekkora és milyen irányú a teljes rendszer által létrehozott mágneses tér a kör középpontjában?
 hosszúságú szigetelőpálca végére elhelyezett kisméretű testet
hosszúságú szigetelőpálca végére elhelyezett kisméretű testet  töltéssel látunk el. A szigetelő nyél másik végét tengelyhez rögzítve
töltéssel látunk el. A szigetelő nyél másik végét tengelyhez rögzítve  szögsebességgel megforgatjuk.
szögsebességgel megforgatjuk.
a) Milyen hatással lesz a körmozgást végző töltött test a környezetére?
b) Mekkora és milyen irányú lesz a mágneses indukció a kör középpontján átmenő, pálya síkjára merőleges tengely mentén?
- Egy R sugarú üvegkorong egyik oldalát
 egyenletes töltéssűrűséggel látjuk el. A korongot a szimmetriatengelye körül
egyenletes töltéssűrűséggel látjuk el. A korongot a szimmetriatengelye körül  szögsebességgel megforgatjuk. Mekkora lesz a mágneses tér a korong tengelyén, a korong síkjától
szögsebességgel megforgatjuk. Mekkora lesz a mágneses tér a korong tengelyén, a korong síkjától  távolságban?
távolságban?
- Határozzuk meg a mágneses indukció nagyságát egy
 hosszúságú,
hosszúságú,  menetű szolenoidban, amelyben
menetű szolenoidban, amelyben  áram folyik gerjesztési törvény segítségével.
áram folyik gerjesztési törvény segítségével.
- Határozzuk meg a mágneses indukció nagyságát egy
 sugarú,
sugarú,  hosszúságú,
hosszúságú,  menetű szolenoidban, amelyben
menetű szolenoidban, amelyben  áram folyik, Biot-Savart törvény segítségével.
áram folyik, Biot-Savart törvény segítségével.
![\[B=\dfrac{\mu_0 I}{4 \pi d} (1-(-1))=\dfrac{\mu_0 I}{2 \pi d}\]](/images/math/8/5/3/853f065bc278c152dca55b624e44abc8.png)
![\[B= \dfrac{\mu_0 I}{2\pi r}\]](/images/math/f/1/0/f10fdea2c59fc782f76c37e7ede59acd.png)
![\[B=\dfrac{\mu_0 I}{4 \pi R} \pi=\dfrac{\mu_0 I}{4 R}\]](/images/math/d/5/3/d53dd483c5b0ce1e917e9632b9c80c50.png)
![\[\vec{H}=H\vec{e}=\dfrac{jr}{2}\dfrac{\vec{j}\times \vec{r}}{jr}=\dfrac{\vec{j}\times \vec{r}}{2}\]](/images/math/3/f/4/3f4c2d9e58755498d5360f21a388d33e.png)
![\[\vec{H}=H\vec{e}=\dfrac{jR^2}{2r}\dfrac{\vec{j}\times \vec{r}}{jr}=\dfrac{R^2}{2r^2} \left(\vec{j}\times \vec{r}\right)\]](/images/math/4/e/2/4e2f3995504fff59133188c2b34afb72.png)
![\[\vec{H}=\dfrac{\vec{j}\times \vec{d}}{2}\]](/images/math/c/f/2/cf254b99805abec89ef44e22cd745dbc.png)
![\[B_A=0\]](/images/math/5/2/4/5249640f86be299e615d5ebf267ff07f.png)
![\[B_B=\dfrac{\mu_0 I}{2\pi d}\]](/images/math/8/9/a/89a5e86989870e8ddb76e3ba252c9e22.png)
![\[B_{C}=B_{C1}+B_{C2}=\dfrac{\mu_0 I}{2\pi \left( d-\dfrac{R}{2}\right)}-\dfrac{\mu_0 I}{4\pi R}= \dfrac{\mu_0 I}{2\pi} \left( \dfrac{1}{ d-\dfrac{R}{2}}-\dfrac{1}{2 R} \right)\]](/images/math/d/6/1/d6119b421afeee0a43f35ab08493c7c5.png)
![\[B=B_1+B_2=\dfrac{\mu_0 U}{4 \pi r^2 \rho}-\dfrac{\mu_0 U}{4 \pi r^2 \rho}=0\]](/images/math/3/7/7/377287a0710ddcb6970511e35a949cdc.png)
![\[H=\dfrac{I a^2}{2 \pi \left( z^2+\left( \dfrac{a}{2} \right)^2\right) \sqrt{z^2+ \dfrac{a^2}{2} }}\]](/images/math/2/9/f/29f32ae2f69ab4b6ceb3d137d6b975e3.png)
 ) a térerősség helyfüggése:
) a térerősség helyfüggése: ![\[H=\dfrac{I}{2\pi a^2} r\]](/images/math/4/5/a/45ac1ecfbedc24d0d14c4c6f28abea7b.png)
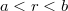 ):
):![\[H=\dfrac{I}{2\pi r}\]](/images/math/9/7/e/97e37ebdd4fa3accb5b02fb8864c462e.png)
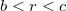 ):
): ![\[H=\dfrac{I}{2\pi r}\dfrac{c^2-r^2}{c^2-b^2}\]](/images/math/e/a/4/ea49738098a748261ba8db7bd7b31436.png)
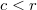 ) a térerősség zérus
) a térerősség zérus ![\[H=0\]](/images/math/b/6/2/b6208659f7d30aadec83d72c69578283.png)
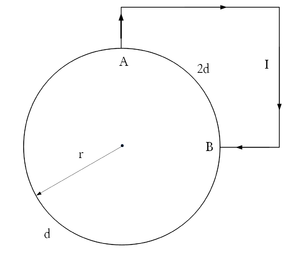
![\[B_{kor}=B_1+B_2=\dfrac{3\mu_0 I}{r}\left( \dfrac{1}{26}-\dfrac{1}{104} \right)=\dfrac{9\mu_0 I}{104r}\]](/images/math/9/0/d/90dbd04a6d8e8eaebfe7fb5f2f5e2fdf.png)
![\[B=0\]](/images/math/1/3/1/131f115805c4a403a4d3c6d67b664c60.png)
![\[B_{negyzet}=2B_3=-\dfrac{\sqrt{2} \mu_0 I}{4 \pi a}\]](/images/math/5/d/3/5d345b02b632185e930ab8a19b8043b7.png)
![\[B_e=B_{kor}+B_{negyzet}=\dfrac{9\mu_0 I}{104r}-\dfrac{\sqrt{2} \mu_0 I}{4 \pi a}\]](/images/math/6/6/c/66c6bda7330c9cddd6ff31000925576a.png)
![\[I=\dfrac{\Delta Q}{\Delta t}=\dfrac{QN \Delta t}{\Delta t}=\dfrac{Q\omega}{2\pi}\]](/images/math/6/9/8/6988dfa2fe80767aefb7fcf889856ca4.png)
![\[B_z=\dfrac{\mu_0 I R^2}{2 (R^2+z^2)^{3/2}}\]](/images/math/3/7/9/3799f1adb400e45e9801c1bd4574df04.png)
![\[B_z=\dfrac{\mu_0 \Omega \omega}{2} \left[ \dfrac{r^2+2z^2}{ (r^2+z^2)^{1/2}} \right]_0^R= \dfrac{\mu_0 \Omega \omega}{2} \left( \dfrac{R^2+2z^2}{ (R^2+z^2)^{1/2}} -2z\right)\]](/images/math/f/8/b/f8b72aadb1a696cc9f2c390167ab863a.png)
![\[B=\dfrac{\mu_0 NI}{l}\]](/images/math/2/0/7/207641385b12448b0305980157b8c127.png)
![\[\lim_{R/l \to 0}B=\lim_{R/l \to 0}\dfrac{\mu_0 NI}{\sqrt{4R^2+l^2}}=\dfrac{\mu_0 NI}{l}\]](/images/math/7/0/8/708e6805e1c5b648b091966e360e2b4f.png)