Elektrosztatika példák - A potenciál töltött fémszállal koaxiális fémhenger esetén

Feladat

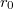1. Egy $\setbox0\hbox{$r_0$}% \message{//depth:\the\dp0//}% \box0%$ sugarú, hosszú egyenes vezető szálra ismeretlen nagyságú töltést viszünk, majd $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú, vékony falú fémhengerrel vesszük körül koaxiálisan. A vezető szálon a felületi töltéssűrűség állandó. 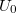A henger töltetlen és a talajtól szigetelt, míg a szál $\setbox0\hbox{$U_{0}$}% \message{//depth:\the\dp0//}% \box0%$ potenciálon van a tengelyétől 1 m távoli ponthoz képest.
   a) Milyen potenciálon lesz a henger?
   b) Mekkora lesz a térerősség a henger külső felületén?
   c) Elektromos mérésekkel kimutatható-e az $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$-nél nagyobb távolságban a henger jelenléte a szál körül?

Megoldás

Egy 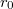$\setbox0\hbox{$r_{0}$}% \message{//depth:\the\dp0//}% \box0%$ sugarú, végtelen, egyenletesen töltött szál körül az elektromos tér:

$\[E = \frac{\omega\cdot r_{0}}{\epsilon_{0}\cdot r}\]$

A potenciál pedig:

$\[U = -\int_{1}^{r}\frac{\omega\cdot r_{0}}{\epsilon_{0}\cdot r}\cdot dr = -\frac{\omega}{\epsilon_{0}}\cdot r_{0}\ln\left(r\right) \]$

Ezzel az ismeretlen töltéssűrűség:

$\[\omega = -\frac{U_{0}\cdot\epsilon_{0}}{r_{0}\cdot\ln\left(r_{0}\right)}\]$

a, A henger potenciálja:

$\[ U = -\frac{\omega}{\epsilon_{0}}\cdot r_{0}\ln\left(R\right)\]$

b, A térerősség a henger külső felületén:

$\[E = \frac{\omega\cdot r_{0}}{\epsilon_{0}\cdot R}\]$

c, Nem, mert a térerősséget nem fogja megváltoztatni, a henger jelenléte. (vö: Gauss-tétel)