Elektrosztatika példák - Egyenletesen töltött fémgömb árnyékolással potenciáltere
A Fizipedia wikiből
Feladat
- Egy
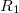 sugarú tömör fémgömböt koncentrikusan vesz körül, egy
sugarú tömör fémgömböt koncentrikusan vesz körül, egy  falvastagságú fém gömbhéj, aminek a belső átmérője
falvastagságú fém gömbhéj, aminek a belső átmérője 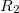 . Közöttük levegő van. A belső fémgömböt feltöltjük, úgy, hogy a felületi töltéssűrűsége
. Közöttük levegő van. A belső fémgömböt feltöltjük, úgy, hogy a felületi töltéssűrűsége  .
.
a) Határozzuk meg a számszerűen a térerősséget a gömbök felszínén.
b) Ábrázoljuk a térerősséget, mint a középponttól mért távolság függvényét, ha a külső gömb földeletlen, illetve földelt.
c) Mekkora a gömbök közötti potenciálkülönbség?
d) Legfeljebb mekkora feszültség kapcsolható a gömbökre, ha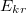 dielektromos szilárdságú szigetelőt teszünk közéjük?
dielektromos szilárdságú szigetelőt teszünk közéjük?
Megoldás
a) Földeletlen esetben a külső gömbön töltésmegosztás jön létre. Ha az 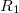 sugarú gömb töltése
sugarú gömb töltése  akkor a külső gömb belső felületén
akkor a külső gömb belső felületén 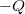 , külső felületén pedig
, külső felületén pedig  töltés jön létre.
töltés jön létre.
A belső gömb felszínére felírva a Gauss-tételt:
![\[E\cdot 4\cdot R_{1}^{2}\cdot\pi = \frac{\omega}{\epsilon_{0}}\cdot 4\cdot R_{1}^{2}\cdot\pi\]](/images/math/5/c/e/5cedb857bd70c0d94d43df39ae9d2a04.png)
![\[E=\frac{\omega}{\epsilon_{0}}\]](/images/math/8/9/b/89b620648d10d395c40cfdf9a669c23f.png)
A külső gömb külső sugara 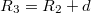 erre felírva a Gauss-tételt:
erre felírva a Gauss-tételt:
![\[E\cdot 4\cdot R_{3}^{2}\cdot\pi = \frac{\omega}{\epsilon_{0}}\cdot 4\cdot R_{1}^{2}\cdot\pi\]](/images/math/0/e/1/0e1bf3d017c40273129cbd2254bfd8df.png)
![\[E=\frac{\omega\cdot R_{1}^{2}}{\epsilon_{0}\cdot R_{3}^{2}}\]](/images/math/3/8/9/3893cc8c6548d0feb6edb3f27eb091f3.png)
b) Különböztessünk meg négy esetet és írjuk fel rájuk a Gauss tételt:
1: 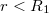
![\[E\cdot 4\cdot r^{2}\cdot\pi = 0 \Rightarrow \vec{E}=0\]](/images/math/0/1/4/014cad340a3928e22bcc5209050ea17b.png)
2: 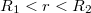
![\[E\cdot 4\cdot r^{2}\cdot\pi = \frac{\omega}{\epsilon_{0}}\cdot 4\cdot R_{1}^{2}\cdot\pi \Rightarrow E= \frac{\omega\cdot R_{1}^{2}}{\epsilon_{0}\cdot r^{2}}\]](/images/math/5/2/9/5296003313ac374ca9327fc15299947c.png)
3: 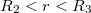
![\[E\cdot 4\cdot r^{2}\cdot\pi = 0 \Rightarrow \vec{E}=0\]](/images/math/0/1/4/014cad340a3928e22bcc5209050ea17b.png)
4.a: (földeletlen): 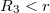
![\[E\cdot 4\cdot r^{2}\cdot\pi = \frac{\omega}{\epsilon_{0}}\cdot 4\cdot R_{1}^{2}\cdot\pi \Rightarrow E= \frac{\omega\cdot R_{1}^{2}}{\epsilon_{0}\cdot r^{2}}\]](/images/math/5/2/9/5296003313ac374ca9327fc15299947c.png)
4.b: (földelet): 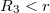
Ekkor annyi töltés jelenik meg a külső gömb külső felszínén, hogy a külső gömb összes töltése 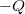 legyen.
legyen.
![\[E\cdot 4\cdot r^{2}\cdot\pi = 0 \Rightarrow \vec{E}=0\]](/images/math/0/1/4/014cad340a3928e22bcc5209050ea17b.png)
c) A gömbök közötti potenciálkülönbség:
![\[\Delta U = -\int_{R_{1}}^{R_{2}}\vec{E}\vec{dr}=-\int_{R_{1}}^{R_{2}}\frac{\omega\cdot R_{1}^{2}}{\epsilon_{0}\cdot r^{2}}\vec{dr}\]](/images/math/d/1/0/d1097c917cad8837bf4aa770c19d7acf.png)
![\[ \Delta U = \frac{\omega\cdot R_{1}^{2}}{\epsilon_{0}}\cdot [\frac{1}{R_{1}}-\frac{1}{R_{2}}]\]](/images/math/f/4/c/f4c60dff9fba2256f157bc2e3afc28c9.png)
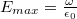 . Ezzel felírva a gömbök közötti potenciálkülönbséget:
. Ezzel felírva a gömbök közötti potenciálkülönbséget: ![\[ \Delta U = E_{max}\cdot R_{1}^{2}\cdot [\frac{1}{R_{1}}-\frac{1}{R_{2}}]\]](/images/math/2/6/4/264dc94494e0f534d43907a26211cc34.png)
A gömbre, akkora potenciálkülönbséget rakhatunk, hogy a kialakuló tér maximális értéke ne legyen nagyobb mint 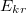 . Ezzel a gömbökre kapcsolható legnagyobb potenciálkülönbség:
. Ezzel a gömbökre kapcsolható legnagyobb potenciálkülönbség:
![\[ \Delta U = E_{kr}\cdot R_{1}^{2}\cdot [\frac{1}{R_{1}}-\frac{1}{R_{2}}]\]](/images/math/5/b/b/5bb8c30ad6998b0a96dd0fe6437d329e.png)