Magnetosztatika példák - Különböző permeabilitású anyagokat tartalmazó szalagpár
Feladat
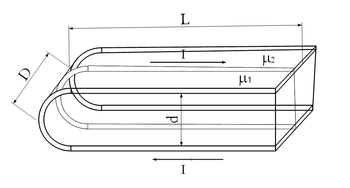
- Mekkora az öninduktivitása az 1. ábrán vázolt
 szélességű,
szélességű,  hosszúságú, egymástól
hosszúságú, egymástól  távolságra levő szalagpárnak, ha a szalagok közötti tér egyik felét
távolságra levő szalagpárnak, ha a szalagok közötti tér egyik felét 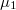 a másik felét
a másik felét 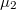 relatív mágneses permeabilitású anyag tölti ki? Tételezzük fel, hogy
relatív mágneses permeabilitású anyag tölti ki? Tételezzük fel, hogy 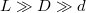
Megoldás
Áramjárta vezető rendszer  öninduktivitása, és az áramok keltette mágneses tér
öninduktivitása, és az áramok keltette mágneses tér 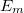 energiája között az alábbi összefüggés írható fel.
energiája között az alábbi összefüggés írható fel.
![\[E_{m}=\dfrac{1}{2}LI^2\]](/images/math/d/3/4/d3413dd5aa07af8f8fde0db6692eff68.png)
Tehát, ha meghatározzuk a tér energiáját, kiszámíthatjuk az öninduktivitást. Ehhez azonban a tér minden pontjában ismernünk kell a mágneses teret.
A 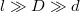 feltételnek köszönhetően az ellentétes irányokba folyó áramoktól átjárt szalagok igen közel vannak egymáshoz, tehát szalagokon kívüli térben indukált mágneses mező már nagyságrendileg
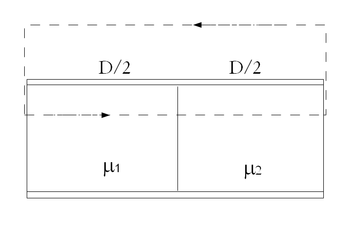
feltételnek köszönhetően az ellentétes irányokba folyó áramoktól átjárt szalagok igen közel vannak egymáshoz, tehát szalagokon kívüli térben indukált mágneses mező már nagyságrendileg  távolságban elhanyagolható értékű. Élhetünk tehát azzal a feltételezéssel, hogy mágneses indukció csak a két lemez közti térben található, valamint azzal, hogy a mágneses tér a két közegben homogén. Ezt kihasználva felvesszük a 2. ábra szerinti zárt görbét, és felírjuk rá az Amper-féle gerjesztési törvényt.
távolságban elhanyagolható értékű. Élhetünk tehát azzal a feltételezéssel, hogy mágneses indukció csak a két lemez közti térben található, valamint azzal, hogy a mágneses tér a két közegben homogén. Ezt kihasználva felvesszük a 2. ábra szerinti zárt görbét, és felírjuk rá az Amper-féle gerjesztési törvényt.
2. ábra
![\[ I= \oint \overline{H}d\overline{l}=H_{1}\dfrac{D}{2}+H_{2}\dfrac{D}{2}\]](/images/math/7/2/d/72d2eb011a7569381907b63c891b917b.png)
Ahol 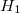 és
és 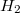 a lemezek közti teret kitöltő, eltérő mágneses permeabilitású közegekben mérhető mágneses térerősség értékei. Tudjuk, hogy a közeghatáron az arra merőleges mágneses indukció folytonosan halad át, ezért a mágneses térerősség nagysága:
a lemezek közti teret kitöltő, eltérő mágneses permeabilitású közegekben mérhető mágneses térerősség értékei. Tudjuk, hogy a közeghatáron az arra merőleges mágneses indukció folytonosan halad át, ezért a mágneses térerősség nagysága:
![\[ H_{1}=\dfrac{B}{\mu_{0}\mu_{1}}\]](/images/math/d/6/9/d6936ad27f9d52e10c21752f21632449.png)
![\[H_{2}=\dfrac{B}{\mu_{0}\mu_{2}}\]](/images/math/1/a/0/1a07807e0af4ddc1e37530446940755d.png)
Helyettesítsük be ezeket a gerjesztési törvénybe:
![\[ I=\dfrac{B}{\mu_{0}\mu_{1}}\dfrac{D}{2}+\dfrac{B}{\mu_{0}\mu_{2}}\dfrac{D}{2}\]](/images/math/c/a/5/ca57921746002cb450b55d392270b8fb.png)
Ebből kifejezhetjük az ismeretlen mágneses indukciót:
![\[ B=\dfrac{2\mu_0 I}{D}\dfrac{\mu_1 \mu_2}{\mu_1 +\mu_2}\]](/images/math/3/7/a/37a59325ddaed095b0dbdf79d7d4b7ab.png)
Ezzel a mágneses térerősségek:
![\[ H_1=\dfrac{2 I}{D}\dfrac{\mu_2}{\mu_1 +\mu_2}\]](/images/math/3/b/7/3b76a6e02cc524f7bd473f313422c27e.png)
![\[ H_2=\dfrac{2 I}{D}\dfrac{\mu_1}{\mu_1 +\mu_2}\]](/images/math/e/3/e/e3ebfe186289add4f2f96c9a5e6b8432.png)
A lemezek közt található két közegben meghatározható a mágneses tér energiasűrűsége:
![\[e_1=\dfrac{1}{2}BH_1=\dfrac{2\mu_0 I^2 \mu_1 \mu_2 ^2}{D^2 (\mu_1+\mu_2)^2} \]](/images/math/7/2/1/72120c4c7541f06df4c6b112f7ea8d54.png)
![\[e_2=\dfrac{1}{2}BH_2=\dfrac{2\mu_0 I^2 \mu_1^2 \mu_2 }{D^2 (\mu_1+\mu_2)^2} \]](/images/math/c/a/3/ca3533fc1d98881e8af3c4c1a53877d6.png)
A tér mágneses energiája így:
![\[ E_m= \int \ edV=e_1 \dfrac{D}{2}ld+e_2 \dfrac{D}{2}ld\]](/images/math/8/5/8/8585bd7dac89184cd6f7ec3c51615089.png)
Behelyettesítve ebbe a fentebb meghatározott 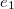 és
és 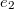 energiasűrűség értékeket megkapjuk a mágneses térben tárolt energiát.
energiasűrűség értékeket megkapjuk a mágneses térben tárolt energiát.
![\[ E_m=\dfrac{I^2 ld \mu_1 \mu_2}{D(\mu_1+\mu_2)}\]](/images/math/a/1/5/a1538a29132c481d50e7786f1cf11173.png)
A tér energiája, és a rendszer öninduktivitása közötti összefüggést felírva az alábbi egyenletet kapjuk:
![\[ E_m=\dfrac{I^2 ld \mu_1 \mu_2}{D(\mu_1+\mu_2)}=\dfrac{1}{2}LI^2\]](/images/math/e/6/f/e6f2acc2f666236baecc25d4d2af3c52.png)
Mely alapján meghatározható az öninduktivitás:
![\[ L=\dfrac{ 2ld \mu_1 \mu_2}{D(\mu_1+\mu_2)}\]](/images/math/3/b/9/3b927ac8777405a6971887687dfb2291.png)