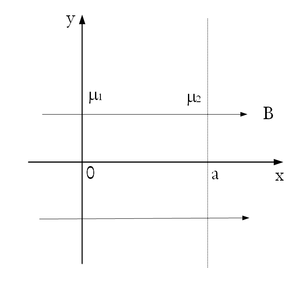
Magnetosztatika példák - Változó relatív permeabilitású lemez körül a mágneses fluxus
A Fizipedia wikiből
Feladat
- Végtelen kiterjedésű,
 vastagságú lemez az 1. ábrának megfelelően
vastagságú lemez az 1. ábrának megfelelően  irányú,
irányú,  indukciójú térben helyezkedik el. A lemez anyagának relatív permeabilitása balról jobbra lineárisan változik
indukciójú térben helyezkedik el. A lemez anyagának relatív permeabilitása balról jobbra lineárisan változik 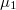 -ről
-ről 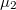 -re.
-re.
a) Határozzuk meg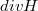 -t
-t  függvényében!
függvényében!
b) Mekkora a térerősség fluxusa egy
térerősség fluxusa egy  tengelyű hengerre, amelynek
tengelyű hengerre, amelynek  területű alap és fedőköre
területű alap és fedőköre 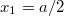 és
és 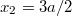 helyen van?
helyen van?
Megoldás
a)
A mágneses indukció a közeghatárokon mindenütt merőlegesen halad át, ezért kijelenthetjük, hogy  értéke mindenütt egyforma. A mágneses térerősség értéke pedig:
értéke mindenütt egyforma. A mágneses térerősség értéke pedig:
![\[H(x)=\dfrac{B}{\mu_0\mu_x}\]](/images/math/5/0/b/50bda747e803bed52849ddf16a3de771.png)
Ismerve a mágneses permeabilitás helyfüggését:
![\[\mu_x=\mu_1+\dfrac{x}{a}(\mu_2-\mu_1)\]](/images/math/2/9/0/290b82371e66a3ee15a8cac44a81bbd5.png)
Meghatározhatjuk a mágneses térerősséget:
![\[H(x)=\dfrac{B}{\mu_0\left( \mu_1+\dfrac{x}{a}(\mu_2-\mu_1) \right)}\]](/images/math/1/a/f/1afa8c5d034872b5bd4d4c6d101e471c.png)
Egydimenziós probléma esetén a mágneses térerősség divergenciája egyszerűen számítható:
![\[divH=\dfrac{dH}{dx}=-\dfrac{\dfrac{B(\mu_2-\mu_1)}{a\mu_0}}{\left( \mu_1+\dfrac{x}{a}(\mu_2-\mu_1)\right)^2}\]](/images/math/1/7/b/17be334635fbcaf47f513b258253ff31.png)
b) A feladatban megadott henger egyik alaplapján a mágneses térerősség értéke:
![\[H(a/2)=\dfrac{B}{\mu_0\left( \mu_1+\dfrac{1}{2}(\mu_2-\mu_1) \right)}=\dfrac{2B}{\mu_0 (\mu_2+\mu_1)}\]](/images/math/b/6/6/b669048009797b1ce67ce555b172df4d.png)
Míg a másik alaplapon a mágneses térerősség egyszerűen:
![\[H(3a/2)=\dfrac{B}{\mu_0}\]](/images/math/2/c/8/2c85ee99a7d08f586f3a44983715c8cc.png)
Hiszen az már az  vastagságú lemezen kívül helyezkedik el. Ezek alapján a mágneses térerősség fluxusa:
vastagságú lemezen kívül helyezkedik el. Ezek alapján a mágneses térerősség fluxusa:
![\[\Phi=\dfrac{SB}{\mu_0}\left( \dfrac{2}{\mu_1+\mu_2} -1\right)\]](/images/math/3/d/c/3dc544ecb6e9149678e1dd4081554882.png)