Magnetosztatika példák - Vasmagos szolenoid mágneses tere 2

Feladat

1. Egy $\setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú, $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú, $\setbox0\hbox{$N$}% \message{//depth:\the\dp0//}% \box0%$ menetű szolenoidban $\setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0%$ erősségű áram folyik. A szolenoidba helyezünk egy ugyanolyan hosszúságú, de 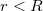$\setbox0\hbox{$r<R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú vashengert, amelynek relatív permeabilitása 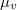$\setbox0\hbox{$\mu_v$}% \message{//depth:\the\dp0//}% \box0%$. Számítsuk ki a tekercs indukciófluxusát!

Megoldás

Szimmetria okokból feltételezzük, hogy a szolenoidban kialakuló mágneses térerősség mindenütt párhuzamos a tekercs tengelyével. Emiatt tekercs belsejében lévő vasmag hengerpalástján a mágneses térerősség a vason belül és kívül is ugyanakkora. ($\setbox0\hbox{$H$}% \message{//depth:\the\dp0//}% \box0%$ felülettel párhuzamos komponense folytonosan megy át a közeghatáron). A tekercsben mérhető $\setbox0\hbox{$H$}% \message{//depth:\the\dp0//}% \box0%$ mágneses térerősséget az Amper-féle gerjesztési törvénnyel határozhatjuk meg:

$\[NI=\oint{}Hdl=Hl\]$

Ebből:

$\[H=\dfrac{NI}{l}\]$

A $\setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0%$ mágneses indukció viszont különbözik a két közegben, ezek értékei a mágneses térerősség ismeretében könnyen számolhatóak:

$\[B_{vas}=\mu_0 \mu_v H=\dfrac{NI\mu_0 \mu_v}{l}\]$

$\[B_{levego}=\mu_0=\dfrac{NI\mu_0}{l}\]$

A vasmag keresztmetszete:

$\[A_{vas}=r^2\pi\]$

Míg a szolenoid vasmag által nem kitöltött részének keresztmetszete:

$\[A_{levego}=R^2\pi-r^2\pi\]$

A szolenoid mágneses indukció fluxusa:

$\[ \Phi=A_{vas}B_{vas}+A_{levego}B_{levego}=\dfrac{NI\mu_0\pi}{l} \left( R^2+r^2(\mu_v-1)\right)\]$