Mechanika - Felharmonikusok Dopplere

Feladat

1. (7.18.) Egy gőzmozdony 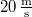$\setbox0\hbox{$20\,\rm{\frac ms}$}% \message{//depth:\the\dp0//}% \box0%$ sebességgel közeledik a megfigyelőhöz. Milyen magasnak hallja egy nyugvó megfigyelő a mozdony sípjának alaphangját, ha azt a mozdonyvezető 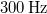$\setbox0\hbox{$300\,\rm{Hz}$}% \message{//depth:\the\dp0//}% \box0%$ rezgésszámúnak hallja? Mennyivel változik meg e síphang felharmonikusainak frekvenciája? ($\setbox0\hbox{$c=330\,\rm{\frac ms}$}% \message{//depth:\the\dp0//}% \box0%$)

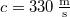Megoldás

A Doppler-hatás összefüggése szerint a mozgó forrásból származó hullám észlelt frekvenciája 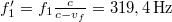$\setbox0\hbox{$f_1'=f_1\frac c{c-v_f}=319,4\,\rm{Hz}$}% \message{//depth:\the\dp0//}% \box0%$, tehát az eltolódás 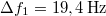$\setbox0\hbox{$\Delta f_1=19,4\,\rm{Hz}$}% \message{//depth:\the\dp0//}% \box0%$. Ha a felharmonikusok frekvenciája 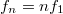$\setbox0\hbox{$f_n=nf_1$}% \message{//depth:\the\dp0//}% \box0%$, akkor az észlelt frekvenciákra is 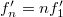$\setbox0\hbox{$f_n'=nf_1'$}% \message{//depth:\the\dp0//}% \box0%$, mivel a nyugvó észlelőt egy szoróztényezővel vesszük figyelembe. 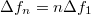Így maga a frekvencia eltolódás a felharmonkusokra $\setbox0\hbox{$\Delta f_n=n\Delta f_1$}% \message{//depth:\the\dp0//}% \box0%$.