Mechanika - Hullámfüggvény 2.
A Fizipedia wikiből
Feladat
- (7.3.) Egy húron csillapítatlan transzverzális hullám terjed
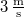 sebességgel pozitív irányban. Amplitúdója
sebességgel pozitív irányban. Amplitúdója 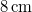 , frekvenciája
, frekvenciája 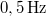 . A
. A  időpillanatban
időpillanatban 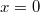 helyen levő részecske kitérése
helyen levő részecske kitérése 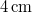 és negatív irányban mozog. Mekkora a kitérése az
és negatív irányban mozog. Mekkora a kitérése az 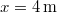 helyen levő részecskének
helyen levő részecskének 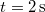 időpillanatban?
időpillanatban?
Megoldás
Legyen a hullámfüggvény alakja![\[y(x,t)=A\sin(\omega t-kx+\phi)\]](/images/math/8/2/a/82a4c06ff0803b8ba0f7c130d6e56683.png)
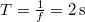 , a hullámhossz pedig
, a hullámhossz pedig 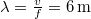 . A kezdeti és peremfeltétel
. A kezdeti és peremfeltétel ![\[y(0,0)=A\sin\phi=0,08\sin\phi=0,04\]](/images/math/d/9/0/d90caf230ccb8de51954ff667511c69a.png)
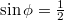 . Ennek két különböző megoldása lehetséges,
. Ennek két különböző megoldása lehetséges, 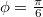 és
és 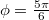 . Mivel kezdetben a részecske negatív irányban mozog, ezért
. Mivel kezdetben a részecske negatív irányban mozog, ezért ![\[v_y=\dot y(x,t)=A\omega\cos(\omega t-kx+\phi)\]](/images/math/3/5/0/350f8257dc2d3af3e9c6d043c29c4928.png)
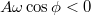 , így
, így 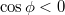 . Ennek
. Ennek 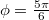 felel meg. Ezt és a periódusidőt felhasználva
felel meg. Ezt és a periódusidőt felhasználva ![\[y(4,2)=y(4,0)=A\sin(0-\frac{2\pi}{\lambda}4+\frac{5\pi}6)=0,08\sin(\frac{5\pi}6-\frac{4\pi}3)=0,08\sin(-\frac{\pi}2)=-0,08\,\rm m=-8\,\rm{cm}\]](/images/math/2/1/d/21decae393c7ba6a700cd77687712954.png)