„Magnetosztatika példák - Koaxiális kábel öninduktivitása” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 2. Kategória:Szerkesztő:Beleznai Kategória:Magnetosztatika {{Kísérleti fizika gyakorlat | tárgynév …”) |
(→Megoldás) |
||
| 16. sor: | 16. sor: | ||
$$I=\oint{}Hdl=2r\pi H$$ | $$I=\oint{}Hdl=2r\pi H$$ | ||
| − | Ebből a hengerszimmetrikus mágneses | + | Ebből a hengerszimmetrikus mágneses tér nagyságát meghatározhatjuk a tengelytől mért távolság függvényében: |
$$H=\dfrac{I}{2\pi r}$$ | $$H=\dfrac{I}{2\pi r}$$ | ||
A lap 2013. szeptember 15., 15:19-kori változata
Feladat
- Adott egy
 hosszúságú koaxiális hengerpár. A belső,
hosszúságú koaxiális hengerpár. A belső, 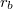 sugarú hengerfelületen
sugarú hengerfelületen  áram folyik a tengely irányában, míg a külső,
áram folyik a tengely irányában, míg a külső, 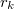 sugarú felületen ugyanakkora, de ellentétes irányú áram folyik. Számítsuk ki a rendszer öninduktivitását!
sugarú felületen ugyanakkora, de ellentétes irányú áram folyik. Számítsuk ki a rendszer öninduktivitását!
Megoldás
Először határozzuk meg a rendszer által indukált mágneses teret! Vegyünk fel egy 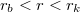 sugarú kört a hengerekével egybeeső tengellyel. Írjuk fel erre a zárt görbére az Amper-féle gerjesztési törvényt!
sugarú kört a hengerekével egybeeső tengellyel. Írjuk fel erre a zárt görbére az Amper-féle gerjesztési törvényt!
![\[I=\oint{}Hdl=2r\pi H\]](/images/math/c/3/b/c3b723b01489a769558b5d11c9bfdf79.png)
Ebből a hengerszimmetrikus mágneses tér nagyságát meghatározhatjuk a tengelytől mért távolság függvényében:
![\[H=\dfrac{I}{2\pi r}\]](/images/math/9/7/e/97e37ebdd4fa3accb5b02fb8864c462e.png)
Az Amper-féle gerjesztési törvény segítségével könnyen belátható, hogy a két hengeren kívül (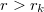 ) a mágneses tér zérus. Ebből következik, hogy mágneses indukció csak a két henger közötti térben van, melynek fluxusa a következőképp számítható, ha tudjuk, hogy
) a mágneses tér zérus. Ebből következik, hogy mágneses indukció csak a két henger közötti térben van, melynek fluxusa a következőképp számítható, ha tudjuk, hogy 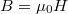 :
:
![\[\Phi=\int{}BdA=l\int_{r_b}^{r_k}B_{r}dr=\dfrac{\mu_0 l I}{2\pi}\int_{r_b}^{r_k}\dfrac{1}{r}dr=\dfrac{\mu_0 l I}{2\pi}ln\left( \dfrac{r_k}{r_b} \right)\]](/images/math/b/e/5/be53b6bec12c4d03f66d953c177c27a1.png)
A rendszer önindukciója:
![\[L=\dfrac{\Phi}{I}=\dfrac{\mu_0 l}{2\pi}ln\left( \dfrac{r_k}{r_b} \right)\]](/images/math/2/9/7/297098928cbccf0502612f516f6e4011.png)