„Magnetosztatika példák - Vasmagos szolenoid mágneses tere” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 2. Kategória:Szerkesztő:Beleznai Kategória:Magnetosztatika {{Kísérleti fizika gyakorlat | tárgynév …”)
 
(→‎Megoldás)
 
(egy szerkesztő 2 közbeeső változata nincs mutatva)
8. sor: 8. sor:
 
}}
 
}}
 
== Feladat ==
 
== Feladat ==
−
</noinclude><wlatex>#Egy $l$ hosszúságú, $r$ sugarú, $N$ menetű szolenoidban $I$ erősségű áram folyik. A szolenoidba helyezünk egy ugyanolyan keresztmetszetű, $h<l$ hosszúságú vashengert, amelynek relatív permeabilitása $\mu_v$. Számítsuk ki a mágneses térerősség és a mágneses indukció értékét a vason belül és kívül! </wlatex><includeonly><wlatex>{{Végeredmény|content=$$H_{vas}=\dfrac{ NI}{h\left( 1-\mu_v \right)+l\mu_v} $$
+
</noinclude><wlatex>#Egy $l$ hosszúságú, $r$ sugarú, $N$ menetű szolenoidban $I$ erősségű áram folyik. A szolenoidba helyezünk egy ugyanolyan keresztmetszetű, $h<l$ hosszúságú vashengert, amelynek relatív permeabilitása $\mu_v$. Számítsuk ki a mágneses térerősség és a mágneses indukció értékét a vason belül és kívül! </wlatex><includeonly><wlatex>{{Végeredmény|content=$$H_{vas}=\dfrac{ NI}{h\left( 1-\mu_v \right)+l\mu_v} $$$$H_{levego}=\dfrac{ NI}{h\left( \dfrac{1}{\mu_v}-1 \right)+l} $$}}
−
$$H_{levego}=\dfrac{ NI}{h\left( \dfrac{1}{\mu_v}-1 \right)+l} $$}}
+
 
</wlatex></includeonly><noinclude>
 
</wlatex></includeonly><noinclude>
 
== Megoldás ==
 
== Megoldás ==
18. sor: 17. sor:
 
$$H_{levego}=\dfrac{B}{\mu_0}$$
 
$$H_{levego}=\dfrac{B}{\mu_0}$$
 
    
 
    
−
Felvéve az 1. ábra szerinti zárt görbét, a mágneses térerősségekre felírható az Amper-féle gerjesztési törvény:
+
Vegyünk fel egy zárt görbét, mely végighalad a szolenoid tengelye mentén, majd a tekercsen kívül, attól nagy távolságban záródik. A zárt görbére írjuk fel az Amper-féle gerjesztési törvényt:
  
−
$$NI=\oint{}Hdl=H_{vas}h+H_{levego}(l-h)=\dfrac{B}{\mu_0} \left( \dfrac{h}{\mu_v}+(l-h) \right)$$
+
$$NI=\oint{}Hdl\approx H_{vas}h+H_{levego}(l-h)=\dfrac{B}{\mu_0} \left( \dfrac{h}{\mu_v}+(l-h) \right)$$
  
 
Ebből kifejezve a mágneses indukciót:
 
Ebből kifejezve a mágneses indukciót:

A lap jelenlegi, 2013. szeptember 30., 15:16-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 2.
Gyakorlatok listája:
  1. Erőhatások elektromos erőtérben, elektromos térerősség
  2. Elektromos potenciál
  3. Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok
  4. Kapacitás, kondenzátorok. Elrendezések energiája
  5. Vezetőképesség, áramsűrűség
  6. Biot-Savart törvény, gerjesztési törvény
  7. Erőhatások mágneses térben
  8. Mágneses térerősség. Kölcsönös és öninduktivitás
  9. Az indukció törvénye, mozgási indukció
  10. Mágneses tér energiája. Váltakozó áram, eltolási áram
Magnetosztatika - Mágneses térerősség. Kölcsönös és öninduktivitás
Feladatok listája:
  1. B és H fluxusa mágneses anyag jelenlétében
  2. Változó relatív permeabilitású lemez körül a mágneses fluxus
  3. Toroid mágneses tere
  4. Vasmagos szolenoid mágneses tere
  5. Vasmagos szolenoid mágneses tere 2
  6. Szolenoid tekercs öninduktivitása
  7. Koaxiális kábel öninduktivitása
  8. Tömör hengeres vezető öninduktivitása
  9. Négyzet keresztmetszetű toroid tekercs öninduktivitása
  10. Párhuzamos henger alakú vezetőpár öninduktivitása
  11. Egyenes vezető és vezető keret közti kölcsönös induktivitás
  12. Négyzetes keresztmetszetű toroid forgástengelyében hosszú egyenes vezetővel
  13. Koncentrikus körvezetők öninduktivitása
  14. Két különböző permeabilitású anyagot tartalmazó koaxiális kábel
  15. Toroid tekercs légréses vasmaggal
  16. Különböző permeabilitású anyagokat tartalmazó szalagpár
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

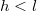  1. Egy \setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0% hosszúságú, \setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0% sugarú, \setbox0\hbox{$N$}% \message{//depth:\the\dp0//}% \box0% menetű szolenoidban \setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0% erősségű áram folyik. A szolenoidba helyezünk egy ugyanolyan keresztmetszetű, \setbox0\hbox{$h<l$}% \message{//depth:\the\dp0//}% \box0% hosszúságú vashengert, amelynek relatív permeabilitása 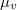\setbox0\hbox{$\mu_v$}% \message{//depth:\the\dp0//}% \box0%. Számítsuk ki a mágneses térerősség és a mágneses indukció értékét a vason belül és kívül!

Megoldás


Szimmetria okokból feltételezzük, hogy a szolenoidban kialakuló mágneses indukció mindenütt párhuzamos a tekercs tengelyével. Ebben az esetben a mágneses indukció a vasmag közeghatárain merőlegesen halad át, tehát nagysága a tekercsen belül konstans \setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0% értékűnek tekinthető. Ebből következik, hogy a \setbox0\hbox{$H$}% \message{//depth:\the\dp0//}% \box0% mágneses tér viszont a két közegben eltérő:

\[H_{vas}=\dfrac{B}{\mu_0 \mu_v}\]
\[H_{levego}=\dfrac{B}{\mu_0}\]

Vegyünk fel egy zárt görbét, mely végighalad a szolenoid tengelye mentén, majd a tekercsen kívül, attól nagy távolságban záródik. A zárt görbére írjuk fel az Amper-féle gerjesztési törvényt:

\[NI=\oint{}Hdl\approx H_{vas}h+H_{levego}(l-h)=\dfrac{B}{\mu_0} \left( \dfrac{h}{\mu_v}+(l-h) \right)\]

Ebből kifejezve a mágneses indukciót:

\[B=\dfrac{\mu_0 NI}{h\left( \dfrac{1}{\mu_v}-1 \right)+l} \]

Az ismert mágneses indukció értékét behelyettesítve a térerősség korábban felírt összefüggéseibe, megkapjuk a térerősségeket:

\[H_{vas}=\dfrac{ NI}{h\left( 1-\mu_v \right)+l\mu_v} \]
\[H_{levego}=\dfrac{ NI}{h\left( \dfrac{1}{\mu_v}-1 \right)+l} \]
A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Magnetosztatika_példák_-_Vasmagos_szolenoid_mágneses_tere&oldid=13069”