„Termodinamika példák - Dinamikus fűtés hőszivattyúval” változatai közötti eltérés

A Fizipedia wikiből
(→‎Megoldás)
a (Szöveg koherenssé tétele)
 
(egy szerkesztő 2 közbeeső változata nincs mutatva)
3. sor: 3. sor:
 
[[Kategória:Szerkesztő:Stippinger]]
 
[[Kategória:Szerkesztő:Stippinger]]
 
[[Kategória:Termodinamika]]
 
[[Kategória:Termodinamika]]
−
[[Kategória:Termodinamika - Kinetikus gázelmélet, transzportfolyamatok]]
 
 
{{Kísérleti fizika gyakorlat
 
{{Kísérleti fizika gyakorlat
 
| tárgynév    = Kísérleti fizika 3. gyakorlat
 
| tárgynév    = Kísérleti fizika 3. gyakorlat
12. sor: 11. sor:
 
## A fűtőanyagot elégetjük egy hőerőgép tűzszekrényében, melynek hőmérsékletét állandó $T_1$ hőmérsékleten tartjuk (ez a hőerőgép felső hőtartálya).
 
## A fűtőanyagot elégetjük egy hőerőgép tűzszekrényében, melynek hőmérsékletét állandó $T_1$ hőmérsékleten tartjuk (ez a hőerőgép felső hőtartálya).
 
## A hőerőgép egy hőszivattyút működtet, amelynek alsó hőtartálya egy tó $T_2$ hőmérsékletű vize, felső hőtartálya pedig a hőerőgépet hűtő $T$ hőmérsékletű víz, amely az épületet egyúttal fűti ($T_1>T>T_2$).
 
## A hőerőgép egy hőszivattyút működtet, amelynek alsó hőtartálya egy tó $T_2$ hőmérsékletű vize, felső hőtartálya pedig a hőerőgépet hűtő $T$ hőmérsékletű víz, amely az épületet egyúttal fűti ($T_1>T>T_2$).
−
#: A tűzszekrényben $q$ égéshőjű anyag ég, a hőerőgép és a hőszivattyú veszteség nélkül Carnot--hatásfokkal működik. Határozzuk meg, mennyi hőt kap a helyiség egységnyi tömegű fűtőanyag elégetése árán!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$Q=q\frac{1-T_2/T_1}{1-T_2/T}>q.$$}}</wlatex></includeonly><noinclude>
+
#: A tűzszekrényben $q$ égéshőjű anyag ég, a hőerőgép és a hőszivattyú veszteség nélkül, Carnot-hatásfokkal működik. Határozzuk meg, mennyi hőt kap a helyiség egységnyi tömegű fűtőanyag elégetése árán!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$Q=q\frac{1-T_2/T_1}{1-T_2/T}>q.$$}}</wlatex></includeonly><noinclude>
 +
 
 
== Megoldás ==
 
== Megoldás ==
−
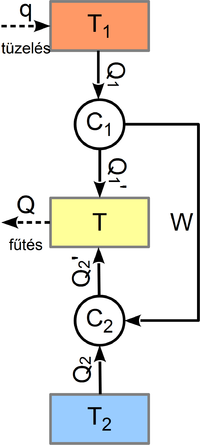
<wlatex>[[Fájl:Termodinamika - Dinamikus fűtés.png|thumb|left|150px|A dinamikus fűtési elrendezés]]
+
<wlatex>[[Fájl:Termodinamika - Dinamikus fűtés.png|thumb|left|200px|A dinamikus fűtési elrendezés]]
 
'''A $C_1$ körfolyamat''' által termelt munka
 
'''A $C_1$ körfolyamat''' által termelt munka
−
$$W=Q_1-|Q_1'|,$$
+
$$ W = Q_1-|Q_1'|, $$
 
a körfolyamat hatásfoka pedig
 
a körfolyamat hatásfoka pedig
−
$$\eta_1=\frac{W}{Q_1}=1-\frac{|Q_1'|}{Q_1}=1-\frac{T}{T_1}.$$
+
$$ \eta_1 = \frac{W}{Q_1}
 +
    = 1-\frac{|Q_1'|}{Q_1}
 +
    = 1-\frac{T}{T_1}. $$
 
Kifejezve a lakásnak átadott $Q_1'$ maradványhőt
 
Kifejezve a lakásnak átadott $Q_1'$ maradványhőt
−
$$|Q_1'|=Q_1\frac{T}{T_1}$$
+
$$ |Q_1'| = Q_1\frac{T}{T_1} $$
 
a munka kifejezése egyszerűsödik:
 
a munka kifejezése egyszerűsödik:
−
$$W=Q_1\left(1-\frac{T}{T_1}\right).$$
+
$$ W = Q_1\left(1-\frac{T}{T_1}\right). $$
 
Mivel a felső hőtartályt állandó hőmérsékletűnek tartjuk $Q_1=q$.
 
Mivel a felső hőtartályt állandó hőmérsékletűnek tartjuk $Q_1=q$.
  
 
'''A $C_2$ körfolyamat''' hatásfoka
 
'''A $C_2$ körfolyamat''' hatásfoka
−
$$\eta_2=\frac{W}{|Q_2'|}=1-\frac{T_2}{T}$$
+
$$ \eta_2 = \frac{W}{|Q_2'|}
−
segítségével a fűtésre juttatott hő kifejezhető:
+
    = 1-\frac{T_2}{T}, $$
−
$$|Q_2'|=\frac{W}{1-\frac{T_2}{T}}=Q_1\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}$$
+
aminek segítségével a fűtésre juttatott hő kifejezhető:
 +
$$ |Q_2'| = \frac{W}{1-\frac{T_2}{T}}
 +
    = Q_1\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}. $$
  
 
'''A teljes rendszer''' fűtőteljesítménye
 
'''A teljes rendszer''' fűtőteljesítménye
−
$$Q=|Q_1'|+|Q_2'|=Q_1\left(\frac{T}{T_1}+\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}\right)=
+
$$ Q = |Q_1'|+|Q_2'|
−
Q_1\left(\frac{\frac{T}{T_1}-\frac{T_2}{T_1}}{1-\frac{T_2}{T}}+\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}\right)=
+
    = Q_1 \left(\frac{T}{T_1}+\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}\right)
−
Q_1\frac{1-\frac{T_2}{T_1}}{1-\frac{T_2}{T}}>q$$
+
    = Q_1 \left(\frac{\frac{T}{T_1}-\frac{T_2}{T_1}}{1-\frac{T_2}{T}}+\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}\right)
 +
    = Q_1 \frac{1-\frac{T_2}{T_1}}{1-\frac{T_2}{T}}>q, $$
 
hiszen $T_1>T>T_2$.
 
hiszen $T_1>T>T_2$.
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap jelenlegi, 2013. május 4., 14:34-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Termodinamika - Fajhő, Körfolyamatok
Feladatok listája:
  1. Id. g. állapotváltozása egyenlettel
  2. Id. g. állandó mólhőjű folyamatai
  3. Id. g. állapotváltozása p-V összefüggéssel
  4. Id. g. körfolyamatai és
  5. munkája
  6. Id. g. egy körfolyamata izotermával
  7. Carnot-hűtőgép
  8. Id. g. egy körfolyamata adiabatával
  9. Id. g. körfolyamata: izob. és adiab.
  10. Dinamikus fűtés hőszivattyúval
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

  1. Egy épület fűtésére az ún. dinamikus fűtést használjuk:
    1. A fűtőanyagot elégetjük egy hőerőgép tűzszekrényében, melynek hőmérsékletét állandó \setbox0\hbox{$T_1$}% \message{//depth:\the\dp0//}% \box0% hőmérsékleten tartjuk (ez a hőerőgép felső hőtartálya).
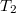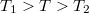    2. A hőerőgép egy hőszivattyút működtet, amelynek alsó hőtartálya egy tó \setbox0\hbox{$T_2$}% \message{//depth:\the\dp0//}% \box0% hőmérsékletű vize, felső hőtartálya pedig a hőerőgépet hűtő \setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0% hőmérsékletű víz, amely az épületet egyúttal fűti (\setbox0\hbox{$T_1>T>T_2$}% \message{//depth:\the\dp0//}% \box0%).
    A tűzszekrényben \setbox0\hbox{$q$}% \message{//depth:\the\dp0//}% \box0% égéshőjű anyag ég, a hőerőgép és a hőszivattyú veszteség nélkül, Carnot-hatásfokkal működik. Határozzuk meg, mennyi hőt kap a helyiség egységnyi tömegű fűtőanyag elégetése árán!

Megoldás

A 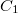dinamikus fűtési elrendezés

A \setbox0\hbox{$C_1$}% \message{//depth:\the\dp0//}% \box0% körfolyamat által termelt munka

\[ W = Q_1-|Q_1'|, \]

a körfolyamat hatásfoka pedig

\[ \eta_1 = \frac{W}{Q_1} = 1-\frac{|Q_1'|}{Q_1} = 1-\frac{T}{T_1}. \]

Kifejezve a lakásnak átadott 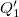\setbox0\hbox{$Q_1'$}% \message{//depth:\the\dp0//}% \box0% maradványhőt

\[ |Q_1'| = Q_1\frac{T}{T_1} \]

a munka kifejezése egyszerűsödik:

\[ W = Q_1\left(1-\frac{T}{T_1}\right). \]

Mivel a felső hőtartályt állandó hőmérsékletűnek tartjuk 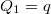\setbox0\hbox{$Q_1=q$}% \messa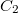ge{//depth:\the\dp0//}% \box0%.

A \setbox0\hbox{$C_2$}% \message{//depth:\the\dp0//}% \box0% körfolyamat hatásfoka

\[ \eta_2 = \frac{W}{|Q_2'|} = 1-\frac{T_2}{T}, \]

aminek segítségével a fűtésre juttatott hő kifejezhető:

\[ |Q_2'| = \frac{W}{1-\frac{T_2}{T}} = Q_1\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}. \]

A teljes rendszer fűtőteljesítménye

\[ Q = |Q_1'|+|Q_2'| = Q_1 \left(\frac{T}{T_1}+\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}\right) = Q_1 \left(\frac{\frac{T}{T_1}-\frac{T_2}{T_1}}{1-\frac{T_2}{T}}+\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}\right) = Q_1 \frac{1-\frac{T_2}{T_1}}{1-\frac{T_2}{T}}>q, \]

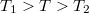hiszen \setbox0\hbox{$T_1>T>T_2$}% \message{//depth:\the\dp0//}% \box0%.

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Termodinamika_példák_-_Dinamikus_fűtés_hőszivattyúval&oldid=9807”