„Mechanika - Hullámfüggvény 1.” változatai közötti eltérés
A Fizipedia wikiből
a |
|||
| 5. sor: | 5. sor: | ||
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika gyakorlat 1. | | tárgynév = Kísérleti fizika gyakorlat 1. | ||
| − | | témakör = Mechanika - | + | | témakör = Mechanika - Hullámok |
}} | }} | ||
== Feladat == | == Feladat == | ||
A lap jelenlegi, 2016. május 11., 13:55-kori változata
Feladat
- (S-Je8 16.18) Egy húron terjedő transzverzális szinuszos hullám periódusideje
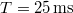, és 
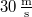sebességgel halad 
irányban. Az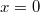 
pont kitérése 
-ban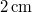 
, sebessége 
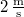. Mekkora a hullám amplitúdója? Mekkora a kezdőfázisa? Írjuk fel a hullámfüggvényt!
Megoldás
A hullám függvény felírásához szükséges a körfrekvencia és a hullámszám:![\[\omega=\frac{2\pi}T=80\pi\,\rm s\]](/images/math/6/2/d/62defc0320051da1eab7d66de543d65d.png)
![\[k=\frac{\omega}c=8,38\,\rm{\frac 1m}\]](/images/math/4/9/d/49d85302848a0e7be775da4570b1cdaf.png)
![\[A=\sqrt{x_0^2+\frac{v_0^2}{\omega^2}}=2,15\,\rm{cm}\]](/images/math/b/9/3/b9376a8757f3c403443d404347937609.png)
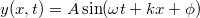alakban keressük, ![\[x_0=y(0,0)=A\sin\phi=0,02\,\rm m\]](/images/math/b/a/e/baebc5b2bf138b8ba8521b8cd2bc6303.png)
![\[v_0=\dot y(0,0)=A\omega\cos\phi,\]](/images/math/9/b/9/9b9e345dfecba80839e8f3a8a93b22eb.png)
![\[\tan\phi=\frac{x_0\omega}{v_0}\]](/images/math/4/5/d/45d826c8216a610afc876e75644e68af.png)
![\[\phi=-1,192+n\pi\]](/images/math/a/f/b/afba288d539fb169f449b006ca421f4f.png)
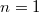, azaz 
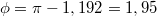radiánban. Végül a hullámfüggvény SI egségekben: ![\[y(x,t)=0,0215\sin(80\pi\,t+8,38x+1,95)\]](/images/math/8/b/c/8bccb2c6721257aecd2b946b9944eb7f.png)
