„Termodinamika példák - Ideális gáz körfolyamatai” változatai közötti eltérés
A Fizipedia wikiből
a (Szöveg koherenssé tétele.) |
|||
| (egy szerkesztő 4 közbeeső változata nincs mutatva) | |||
| 6. sor: | 6. sor: | ||
| tárgynév = Kísérleti fizika 3. gyakorlat | | tárgynév = Kísérleti fizika 3. gyakorlat | ||
| témakör = Termodinamika - Fajhő, Körfolyamatok | | témakör = Termodinamika - Fajhő, Körfolyamatok | ||
| + | | rövid = Fajhő, Körfolyamatok | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Az első ábrán egy ideális gázzal végzett körfolyamat $p-V$ diagramja látható. Ábrázoljuk a folyamatot $ | + | </noinclude><wlatex># Az első ábrán egy ideális gázzal végzett körfolyamat $p-V$ diagramja látható. Ábrázoljuk a folyamatot $T-V$ és $T-p$ diagramon! |
| − | # A második ábrán egy ideális gázzal végzett körfolyamat $p-V$ diagramja látható. Mekkora a gáz által végzett munka?[[Fájl:Ideális gáz két körfolyamata ábrával.svg]] | + | # A második ábrán egy ideális gázzal végzett körfolyamat $p-V$ diagramja látható. Mekkora a gáz által végzett munka?<br /></wlatex><includeonly>[[Fájl:Ideális gáz két körfolyamata ábrával.svg|400px]]<wlatex>{{Végeredmény|content=$$W=0.$$}}</wlatex></includeonly><noinclude>[[Fájl:Ideális gáz két körfolyamata ábrával ötlet.svg|400px]] |
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A megoldás | + | <wlatex>#* A megadott $p-V$ diagramról az izotermát átvetíthetjük a $T-V$ diagramba. Az izobár vonal itt $T=\frac{p}{nR}V=\mathrm{const.}\cdot V$ origón áthaladó egyenes, a függőleges izochor vonal pedig a két szakaszt köti össze. |
| + | #* További vetítéssel az izobár vonalat átvihetjük a $T-p$ diagramba. Itt az izochor vonal ($T=\frac{V}{nR}p=\mathrm{const.}\cdot p$) lesz origón áthaladó egyenes, az izoterma pedig vízszintes. | ||
| + | #* Az egyes állapotok beazonosításával vagy a vetítés során figyeljük meg a körüljárási irányokat!<br />[[Fájl:Ideális gáz két körfolyamata ábrával megoldás.svg|400px]] | ||
| + | # A második ábrán jelölt körfolyamat két egybevágó, de ellentétes irányítású háromszöggel ábrázolható körfolyamatra bontható, melyek munkáinak előjeles összege a keresett munka. Mivel $p-V$ diagramon $\delta W = p\,\mathrm{d}V$, azért a gáz munkája nagysága a körfolyamat grafikonja által közrezárt területtel egyenlő, előjele pedig a geometriai körüljárási iránnyal ''ellentétes''. Ezekből következik, hogy az egybevágó háromszögek által meghatározott munka az ábrán jelölt módon egyenlő nagyságú, ellentétes előjelű, a teljes körfolyamatban a gáz nem végez munkát. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. május 3., 11:17-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fajhő, Körfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
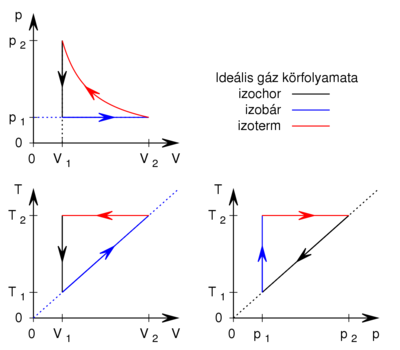
- Az első ábrán egy ideális gázzal végzett körfolyamat
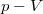diagramja látható. Ábrázoljuk a folyamatot 
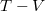és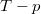 
diagramon!
- A második ábrán egy ideális gázzal végzett körfolyamat 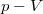diagramja látható. Mekkora a gáz által végzett munka?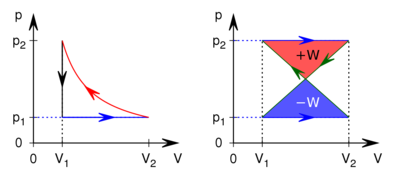
Megoldás
- A megadott 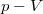diagramról az izotermát átvetíthetjük a 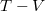diagramba. Az izobár vonal itt
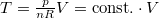origón áthaladó egyenes, a függőleges izochor vonal pedig a két szakaszt köti össze.
- További vetítéssel az izobár vonalat átvihetjük a 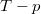diagramba. Itt az izochor vonal (
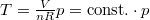) lesz origón áthaladó egyenes, az izoterma pedig vízszintes.
- Az egyes állapotok beazonosításával vagy a vetítés során figyeljük meg a körüljárási irányokat!
- A megadott
- A második ábrán jelölt körfolyamat két egybevágó, de ellentétes irányítású háromszöggel ábrázolható körfolyamatra bontható, melyek munkáinak előjeles összege a keresett munka. Mivel 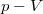diagramon
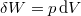, azért a gáz munkája nagysága a körfolyamat grafikonja által közrezárt területtel egyenlő, előjele pedig a geometriai körüljárási iránnyal ellentétes. Ezekből következik, hogy az egybevágó háromszögek által meghatározott munka az ábrán jelölt módon egyenlő nagyságú, ellentétes előjelű, a teljes körfolyamatban a gáz nem végez munkát.
