„Elektrosztatika példák - Párhuzamos végtelen síklapok potenciáltere” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
|||
| 18. sor: | 18. sor: | ||
$$ U =\frac{\omega_{1}}{\epsilon_{0}}\cdot d $$ | $$ U =\frac{\omega_{1}}{\epsilon_{0}}\cdot d $$ | ||
'''b)''' <br> | '''b)''' <br> | ||
| − | Ebben az esetben a földelt lemezen kialakuló felületi töltéssűrűség: $\omega_{3} = -(\omega_{1}+\omega_{2})$ hiszen a földelt lemez helyén, a másik két lemez által okozott térerősség húzza fel a töltéseket a földből.Ebből a | + | Ebben az esetben a földelt lemezen kialakuló felületi töltéssűrűség: $\omega_{3} = -(\omega_{1}+\omega_{2})$ hiszen a földelt lemez helyén, a másik két lemez által okozott térerősség húzza fel a töltéseket a földből.Ebből a térerősség földelt és a betett lemezek között: |
| − | $$E_{1}=\frac{\omega_{1}}{2\cdot\epsilon_{0}}+\frac{\omega_{2}}{2\cdot\epsilon_{0}}-\frac{\omega_{3}}{2\cdot\epsilon_{0}}=\frac{\omega_{1}+\omega_{2}}{ | + | $$E_{1}=\frac{\omega_{1}}{2\cdot\epsilon_{0}}+\frac{\omega_{2}}{2\cdot\epsilon_{0}}-\frac{\omega_{3}}{2\cdot\epsilon_{0}}=\frac{\omega_{1}+\omega_{2}}{\epsilon_{0}}$$ |
| − | + | A betett és a másik lemez között a tér pedig: | |
$$E_{2}=\frac{\omega_{1}}{2\cdot\epsilon_{0}}-\frac{\omega_{2}}{2\cdot\epsilon_{0}}-\frac{\omega_{3}}{2\cdot\epsilon_{0}}=\frac{\omega_{1}}{\epsilon_{0}}$$ | $$E_{2}=\frac{\omega_{1}}{2\cdot\epsilon_{0}}-\frac{\omega_{2}}{2\cdot\epsilon_{0}}-\frac{\omega_{3}}{2\cdot\epsilon_{0}}=\frac{\omega_{1}}{\epsilon_{0}}$$ | ||
Ebből a potenciál különbség: | Ebből a potenciál különbség: | ||
| − | $$U = U_{1}+U_{2} = \frac{\omega_{1}+\omega_{2}}{ | + | $$U = U_{1}+U_{2} = \frac{\omega_{1}+\omega_{2}}{\epsilon_{0}}\cdot \frac{d}{2} + \frac{\omega_{1}}{\epsilon_{0}}\cdot \frac{d}{2} = \frac{2\cdot\omega_{1}+\omega_{2}}{\epsilon_{0}}\cdot \frac{d}{2} $$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. szeptember 24., 16:57-kori változata
Feladat
- Két párhuzamos, nagy kiterjedésű vezető sík egyike földelt, a másik felületi töltéssűrűsége
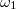 . A lemezek távolsága
. A lemezek távolsága  .
.
a) Mekkora a lemezek közötti potenciálkülönbség?
b) Mekkora lesz a potenciálkülönbség, ha a lemezekkel párhuzamosan, tőlük egyenlő távolságra, egy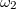 felületi töltéssűrűségű harmadik lemezt helyezünk?
felületi töltéssűrűségű harmadik lemezt helyezünk?
Megoldás
a) A földelt lemezen 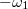 felületi töltéssűrűség alakul ki. A lemezek közötti térerősség nagysága:
felületi töltéssűrűség alakul ki. A lemezek közötti térerősség nagysága:
![\[E=\frac{\omega_{1}}{\epsilon_{0}}\]](/images/math/e/3/1/e31c1f035b1ceaa8ea43fee53bd9a941.png)
Ebből a lemezek közötti potenciálkülönbség:
![\[ U =\frac{\omega_{1}}{\epsilon_{0}}\cdot d \]](/images/math/c/7/9/c7966653df23b09877d552d1a8120db2.png)
b)
Ebben az esetben a földelt lemezen kialakuló felületi töltéssűrűség: 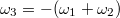 hiszen a földelt lemez helyén, a másik két lemez által okozott térerősség húzza fel a töltéseket a földből.Ebből a térerősség földelt és a betett lemezek között:
hiszen a földelt lemez helyén, a másik két lemez által okozott térerősség húzza fel a töltéseket a földből.Ebből a térerősség földelt és a betett lemezek között:
![\[E_{1}=\frac{\omega_{1}}{2\cdot\epsilon_{0}}+\frac{\omega_{2}}{2\cdot\epsilon_{0}}-\frac{\omega_{3}}{2\cdot\epsilon_{0}}=\frac{\omega_{1}+\omega_{2}}{\epsilon_{0}}\]](/images/math/7/0/8/708da3e353927cd03b13e575f6a9e29a.png)
A betett és a másik lemez között a tér pedig:
![\[E_{2}=\frac{\omega_{1}}{2\cdot\epsilon_{0}}-\frac{\omega_{2}}{2\cdot\epsilon_{0}}-\frac{\omega_{3}}{2\cdot\epsilon_{0}}=\frac{\omega_{1}}{\epsilon_{0}}\]](/images/math/3/4/5/3451d225a9d9622b730423e288add78a.png)
Ebből a potenciál különbség:
![\[U = U_{1}+U_{2} = \frac{\omega_{1}+\omega_{2}}{\epsilon_{0}}\cdot \frac{d}{2} + \frac{\omega_{1}}{\epsilon_{0}}\cdot \frac{d}{2} = \frac{2\cdot\omega_{1}+\omega_{2}}{\epsilon_{0}}\cdot \frac{d}{2} \]](/images/math/4/6/d/46d7021967b564a653e163b97e4f9d3c.png)