„Magnetosztatika példák - Toroid mágneses tere” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
(→Megoldás) |
||
| 23. sor: | 23. sor: | ||
b) | b) | ||
| − | A mágneses térerősségből a mágnesezettséget meghatározhatjuk a | + | A mágneses térerősségből a mágnesezettséget meghatározhatjuk. Ha lineáris anyagról beszélünk, akkor igaz a mágnesezettségre hogy: $$M=\chi H$$. |
| − | + | <br /> | |
| + | Amiből: | ||
$$M=\dfrac{\chi NI}{2\pi R}$$ | $$M=\dfrac{\chi NI}{2\pi R}$$ | ||
A lap jelenlegi, 2013. szeptember 30., 16:14-kori változata
Feladat
 sugarú toroid
sugarú toroid  menetében
menetében  erősségű áram folyik. A toroid
erősségű áram folyik. A toroid  sugarú belsejét
sugarú belsejét 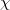 mágneses szuszceptibilitású anyag tölti ki.
mágneses szuszceptibilitású anyag tölti ki.
a) Mekkora a mágneses térerősség?
b) Mekkora a mágnesezettség?
c) Mekkora a mágneses indukció?
Megoldás
a)
A mágneses térerősséget az Amper-féle gerjesztési törvénnyel határozhatjuk meg. Felveszünk egy zárt görbét, mely a tekercs belsejében, a toroidgyűrű középvonalán megy körbe. Feltételezzük, hogy ezen  sugarú kör mentén a mágneses térerősség nagysága állandó. Ezek alapján a gerjesztési törvény:
sugarú kör mentén a mágneses térerősség nagysága állandó. Ezek alapján a gerjesztési törvény:
![\[NI=\oint{}Hdl=2\pi RH\]](/images/math/8/d/8/8d8a8ec5802ff415d240de6448528a35.png)
Kifejezve a térerősség nagyságát:
![\[H=\dfrac{NI}{2\pi R}\]](/images/math/e/f/7/ef7b021524d2766df430c52081ff17ff.png)
b)
A mágneses térerősségből a mágnesezettséget meghatározhatjuk. Ha lineáris anyagról beszélünk, akkor igaz a mágnesezettségre hogy:![\[M=\chi H\]](/images/math/f/7/d/f7d5ef7bbe9e94e317f777e7edc44252.png)
Amiből:
![\[M=\dfrac{\chi NI}{2\pi R}\]](/images/math/7/2/4/724d3ebed60d8e2d94a56adf2db2b72c.png)
c)
A mágneses indukció nagysága kiszámítható 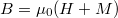 módon:
módon:
![\[B=\dfrac{\mu_0(1+\chi)NI}{2\pi R}\]](/images/math/6/4/d/64d6c1a3711974ae534095ccd93b3624.png)