„Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása2” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „== Feladat == </noinclude><wlatex># Határozzuk meg egy $a$ oldalú, négyzet keresztmetszetű, $N$ menetű toroid tekercs öninduktivitását, ha a tekercs belső sugara …”) |
(→Feladat) |
||
| 1. sor: | 1. sor: | ||
| + | <noinclude> | ||
| + | [[Kategória:Kísérleti fizika gyakorlat 2.]] | ||
| + | [[Kategória:Szerkesztő:Steinbach]] | ||
| + | [[Kategória:Magnetosztatika]] | ||
| + | {{Kísérleti fizika gyakorlat | ||
| + | | tárgynév = Kísérleti fizika gyakorlat 2. | ||
| + | | témakör = Magnetosztatika - Mágneses térerősség. Kölcsönös és öninduktivitás | ||
| + | }} | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># Határozzuk meg egy $a$ oldalú, négyzet keresztmetszetű, $N$ menetű toroid tekercs öninduktivitását, ha a tekercs belső sugara $b$! | </noinclude><wlatex># Határozzuk meg egy $a$ oldalú, négyzet keresztmetszetű, $N$ menetű toroid tekercs öninduktivitását, ha a tekercs belső sugara $b$! | ||
</wlatex><includeonly><wlatex>{{Útmutatás|content=Határozzuk meg a $B$ mágneses térerősséget a tekercs belsejében a tengelytől mért távolság függvényében a gerjesztési törvénysegítségével, számoljuk ki ebből 1 menetre a fluxust, végül az $N$ menet fluxusából határozzuk meg az önindukciós együtthatót!}} {{Végeredmény|content=$L = \frac{\Phi}{I} = \frac{\mu_0 N^2 a}{2 \pi}\, \mathrm{ln} \frac{a+b}{b}.$}} | </wlatex><includeonly><wlatex>{{Útmutatás|content=Határozzuk meg a $B$ mágneses térerősséget a tekercs belsejében a tengelytől mért távolság függvényében a gerjesztési törvénysegítségével, számoljuk ki ebből 1 menetre a fluxust, végül az $N$ menet fluxusából határozzuk meg az önindukciós együtthatót!}} {{Végeredmény|content=$L = \frac{\Phi}{I} = \frac{\mu_0 N^2 a}{2 \pi}\, \mathrm{ln} \frac{a+b}{b}.$}} | ||
</wlatex></includeonly><noinclude> | </wlatex></includeonly><noinclude> | ||
| + | == Megoldás == | ||
| + | <wlatex> | ||
| + | A gerjesztési törvény szerint $$\oint \overrightarrow{B}\overrightarrow{\mathrm{d}r}=\mu_0 N I.$$ | ||
| + | Az integrálási görbét a toroid középkörével koncentrikusan vesszük fel, így $\overrightarrow{B}$ párhuzamos lesz $\overrightarrow{\mathrm{d}r}$-rel, a vektorjelölést elhagyhatjuk. A körszimmetria miatt $B=B(r)$, ezzel az integrálunk egyszerűsödik, és $B(r)$-re a következőt kapjuk: $$B(r)=\frac{\mu_0 N I}{2 r \pi}.$$ | ||
| + | Egy menetre kiszámítva a fluxust: $$\Phi_1=\int_{b}^{a+b} B(r) a \mathrm{d}r = \frac{\mu_0 N I a}{2\pi}\mathrm{ln}\frac{a+b}{b}.$$ | ||
| + | $N$ menetre számítva a fluxust, az ennek $N$-szerese: $\Phi_N = N \Phi_1$<br/> | ||
| + | Az önindukciós tényező tehát $$L=\frac{\Phi_N}{I}=\frac{\mu_0 N^2 a}{2\pi}\mathrm{ln}\frac{a+b}{b}. | ||
| + | |||
| + | </wlatex> | ||
| + | </noinclude> | ||
A lap jelenlegi, 2013. április 26., 15:06-kori változata
Feladat
- Határozzuk meg egy
oldalú, négyzet keresztmetszetű, 
menetű toroid tekercs öninduktivitását, ha a tekercs belső sugara 
!
Megoldás
![\[\oint \overrightarrow{B}\overrightarrow{\mathrm{d}r}=\mu_0 N I.\]](/images/math/6/8/b/68b2535d9e153db358837f30b8598eb3.png)
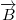párhuzamos lesz 
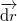-rel, a vektorjelölést elhagyhatjuk. A körszimmetria miatt 
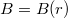, ezzel az integrálunk egyszerűsödik, és 
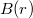-re a következőt kapjuk: ![\[B(r)=\frac{\mu_0 N I}{2 r \pi}.\]](/images/math/4/5/9/459ffe6133311c40e379e4fd8f5af9f3.png)
![\[\Phi_1=\int_{b}^{a+b} B(r) a \mathrm{d}r = \frac{\mu_0 N I a}{2\pi}\mathrm{ln}\frac{a+b}{b}.\]](/images/math/e/7/c/e7c3ea492f1fdeb82d62ad6365bd8167.png)
menetre számítva a fluxust, az ennek -szerese: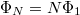 
![\[L=\frac{\Phi_N}{I}=\frac{\mu_0 N^2 a}{2\pi}\mathrm{ln}\frac{a+b}{b}.\]](/images/math/c/f/a/cfa1ff9e4e5e536dcc9a7075ff9e39fa.png)
