„Magnetosztatika - Mágneses térerősség. Kölcsönös és öninduktivitás” változatai közötti eltérés
A Fizipedia wikiből
| 1. sor: | 1. sor: | ||
[[Kategória:Kísérleti fizika gyakorlat 2.]] | [[Kategória:Kísérleti fizika gyakorlat 2.]] | ||
| − | [[Kategória:Szerkesztő: | + | [[Kategória:Szerkesztő:Beleznai]] |
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika gyakorlat 2. | | tárgynév = Kísérleti fizika gyakorlat 2. | ||
| gyaksorszám = 8 | | gyaksorszám = 8 | ||
| − | | témakör = Magnetosztatika - Mágneses térerősség. Kölcsönös és öninduktivitás | + | | témakör = Magnetosztatika - Mágneses térerősség. Kölcsönös és öninduktivitás |
}} | }} | ||
== Feladatok == | == Feladatok == | ||
| − | {{:Magnetosztatika példák - B és H fluxusa mágneses anyag jelenlétében}}{{Megoldás|link=Magnetosztatika példák - B és H fluxusa mágneses anyag jelenlétében}} | + | {{:Magnetosztatika példák - B és H fluxusa mágneses anyag jelenlétében}}{{Megoldás|link=Magnetosztatika példák - B és H fluxusa mágneses anyag |
| − | {{:Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása}}{{Megoldás|link=Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása}} | + | |
| − | {{:Magnetosztatika példák - Négyzetes toroid | + | jelenlétében}} |
| − | {{:Magnetosztatika példák - | + | {{:Magnetosztatika példák - Változó relatív permeabilitású lemez körül a mágneses fluxus}}{{Megoldás|link=Magnetosztatika példák - Változó relatív |
| + | |||
| + | permeabilitású lemez körül a mágneses fluxus}} | ||
| + | {{:Magnetosztatika példák - Toroid mágneses tere}}{{Megoldás|link=Magnetosztatika példák - Toroid mágneses tere}} | ||
| + | {{:Magnetosztatika példák - Vasmagos szolenoid mágneses tere}}{{Megoldás|link=Magnetosztatika példák - Vasmagos szolenoid mágneses tere}} | ||
| + | {{:Magnetosztatika példák - Vasmagos szolenoid mágneses tere 2}}{{Megoldás|link=Magnetosztatika példák - Vasmagos szolenoid mágneses tere 2}} | ||
| + | {{:Magnetosztatika példák - Szolenoid tekercs öninduktivitása}}{{Megoldás|link=Magnetosztatika példák - Szolenoid tekercs öninduktivitása}} | ||
| + | {{:Magnetosztatika példák - Koaxiális hengerpár öninduktivitása}}{{Megoldás|link=Magnetosztatika példák - Koaxiális hengerpár öninduktivitása}} | ||
| + | {{:Magnetosztatika példák - Tömör hengeres vezető öninduktivitása}}{{Megoldás|link=Magnetosztatika példák - Tömör hengeres vezető öninduktivitása}} | ||
| + | {{:Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása}}{{Megoldás|link=Magnetosztatika példák - Négyzetes toroid tekercs | ||
| + | |||
| + | öninduktivitása}} | ||
| + | {{:Magnetosztatika példák - Párhuzamos henger alakú vezetőpár öninduktivitása}}{{Megoldás|link=Magnetosztatika példák - Párhuzamos henger alakú | ||
| + | |||
| + | vezetőpár öninduktivitása}} | ||
| + | {{:Magnetosztatika példák - Egyenes vezető és vezető keret közti kölcsönös induktivitás}}{{Megoldás|link=Magnetosztatika példák - Egyenes vezető és | ||
| + | |||
| + | vezető keret közti kölcsönös induktivitás}} | ||
| + | {{:Magnetosztatika példák - Négyzetes keresztmetszetű toroid forgástengelyében hosszú egyenes vezetővel}}{{Megoldás|link=Magnetosztatika példák - | ||
| + | |||
| + | Négyzetes keresztmetszetű toroid forgástengelyében hosszú egyenes vezetővel}} | ||
| + | {{:Magnetosztatika példák - Koncentrikus körvezetők öninduktivitása}}{{Megoldás|link=Magnetosztatika példák - Koncentrikus körvezetők öninduktivitása}} | ||
| + | {{:Magnetosztatika példák - Koaxiális hengerpár változó permeabilitású anyaggal kitöltve}}{{Megoldás|link=Magnetosztatika példák - Koaxiális hengerpár | ||
| + | |||
| + | változó permeabilitású anyaggal kitöltve}} | ||
| + | {{:Magnetosztatika példák - Toroid tekercs légréses vasmaggal}}{{Megoldás|link=Magnetosztatika példák - Toroid tekercs légréses vasmaggal}} | ||
| + | {{:Magnetosztatika példák - Párhuzamos szalagpár változó permeabilitású anyaggal kitöltve}}{{Megoldás|link=Magnetosztatika példák - KPárhuzamos | ||
| + | |||
| + | szalagpár változó permeabilitású anyaggal kitöltve}} | ||
A lap 2013. július 15., 16:07-kori változata
Feladatok
- A mágneses indukció
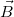 vektorára merőleges sík
vektorára merőleges sík 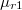 és
és 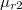 relatív permeabilitású anyagokat választ el egymástól. Tekintsünk egy hengert, melynek
relatív permeabilitású anyagokat választ el egymástól. Tekintsünk egy hengert, melynek  területű körlapjai párhuzamosak a határfelülettel! Határozzuk meg a
területű körlapjai párhuzamosak a határfelülettel! Határozzuk meg a 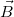 mágneses indukció és a
mágneses indukció és a 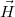 mágneses térerősség fluxusát erre a hengerre! [[Magnetosztatika példák - B és H fluxusa mágneses anyag
mágneses térerősség fluxusát erre a hengerre! [[Magnetosztatika példák - B és H fluxusa mágneses anyag
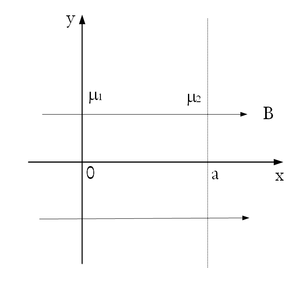
- Végtelen kiterjedésű,
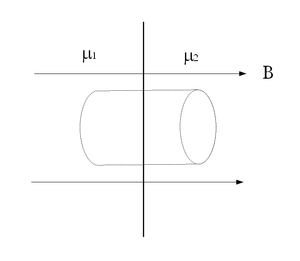
 vastagságú lemez az 1. ábrának megfelelően
vastagságú lemez az 1. ábrának megfelelően  irányú,
irányú,  indukciójú térben helyezkedik el. A lemez anyagának relatív permeabilitása balról jobbra lineárisan változik
indukciójú térben helyezkedik el. A lemez anyagának relatív permeabilitása balról jobbra lineárisan változik 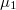 -ről
-ről 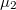 -re.
-re.
a) Határozzuk meg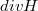 -t
-t  függvényében!
függvényében!
b) Mekkora a térerősség fluxusa egy
térerősség fluxusa egy  tengelyű hengerre, amelynek
tengelyű hengerre, amelynek  területű alap és fedőköre
területű alap és fedőköre 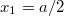 és
és 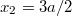 helyen van?
helyen van?
[[Magnetosztatika példák - Változó relatív
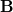 és
és 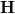 értékét a határfeltétel szerint, és vizsgáljuk meg, mi ad járulékot a fluxus integráljában!
értékét a határfeltétel szerint, és vizsgáljuk meg, mi ad járulékot a fluxus integráljában! 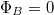
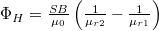
![\[divH=\dfrac{dH}{dx}=-\dfrac{\dfrac{B(\mu_2-\mu_1)}{a\mu_0}}{\left( \mu_1+\dfrac{x}{a}(\mu_2-\mu_1)\right)^2}\]](/images/math/1/7/b/17be334635fbcaf47f513b258253ff31.png)
![\[\Phi=\dfrac{SB}{\mu_0}\left( \dfrac{2}{\mu_1+\mu_2} -1\right)\]](/images/math/3/d/c/3dc544ecb6e9149678e1dd4081554882.png)
 sugarú toroid
sugarú toroid  menetében
menetében  erősségű áram folyik. A toroid
erősségű áram folyik. A toroid  sugarú belsejét
sugarú belsejét 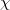 mágneses szuszceptibilitású anyag tölti ki.
mágneses szuszceptibilitású anyag tölti ki. ![\[H=\dfrac{NI}{2\pi R}\]](/images/math/e/f/7/ef7b021524d2766df430c52081ff17ff.png)
![\[M=\dfrac{\chi NI}{2\pi R}\]](/images/math/7/2/4/724d3ebed60d8e2d94a56adf2db2b72c.png)
![\[B=\dfrac{\mu_0(1+\chi)NI}{2\pi R}\]](/images/math/6/4/d/64d6c1a3711974ae534095ccd93b3624.png)
 hosszúságú,
hosszúságú, 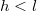 hosszúságú vashengert, amelynek relatív permeabilitása
hosszúságú vashengert, amelynek relatív permeabilitása 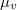 . Számítsuk ki a mágneses térerősség és a mágneses indukció értékét a vason belül és kívül!
. Számítsuk ki a mágneses térerősség és a mágneses indukció értékét a vason belül és kívül! ![\[H_{vas}=\dfrac{ NI}{h\left( 1-\mu_v \right)+l\mu_v} \]](/images/math/6/7/3/6730cbd97b876de3ebcccca9f4c977c1.png)
![\[H_{levego}=\dfrac{ NI}{h\left( \dfrac{1}{\mu_v}-1 \right)+l} \]](/images/math/b/0/d/b0d5b84ff5d21a562d4319522ce4bcb1.png)
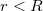 sugarú vashengert, amelynek relatív permeabilitása
sugarú vashengert, amelynek relatív permeabilitása ![\[ \Phi=A_{vas}B_{vas}+A_{levego}B_{levego}=\dfrac{NI\mu_0\pi}{l} \left( R^2+r^2(\mu_v-1)\right)\]](/images/math/2/5/0/2509298a9e4d235a7e8a9dffede56072.png)
 keresztmetszetű szolenoid fluxusát és öninduktivitását!
keresztmetszetű szolenoid fluxusát és öninduktivitását!![\[L=\dfrac{N\Phi}{I}=\dfrac{\mu_0 N^2 A}{l}\]](/images/math/8/e/5/8e54a8ed946b42adec93779cfe4cf850.png)
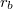 sugarú hengerfelületen
sugarú hengerfelületen 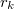 sugarú felületen ugyanakkora, de ellentétes irányú áram folyik. Számítsuk ki a rendszer öninduktivitását!
sugarú felületen ugyanakkora, de ellentétes irányú áram folyik. Számítsuk ki a rendszer öninduktivitását! ![\[L=\dfrac{\Phi}{I}=\dfrac{\mu_0 l}{2\pi}ln\left( \dfrac{r_k}{r_b} \right)\]](/images/math/2/9/7/297098928cbccf0502612f516f6e4011.png)
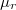 )
) ![\[\Phi=\dfrac{\mu_0 l I}{4\pi}\]](/images/math/9/f/c/9fcde8b3bcbd4214a337f80155023f86.png)
![\[L=\dfrac{\Phi}{I}=\dfrac{\mu_0 l}{4\pi}\]](/images/math/7/2/1/72118da80c69bc079f976d8be6a8a6fe.png)
 !
!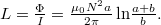
 távolságra vannak egymástól?
távolságra vannak egymástól? ![\[L=L_1+2L_2=\dfrac{\mu_0 l}{\pi} ln \left( \dfrac{d-R}{R} \right)+\dfrac{\mu_0 l}{2\pi}\]](/images/math/2/7/9/2796ef6098223b4acf0bffa730b93b79.png)
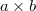 oldalhosszúságú, téglalap alakú vezető keret síkjában az
oldalhosszúságú, téglalap alakú vezető keret síkjában az ![\[L=\dfrac{N\Phi}{I}=\dfrac{\mu_0 Na}{2\pi} ln \left( \dfrac{d+a}{d} \right)\]](/images/math/9/4/b/94b016c2f7fd9515af770862d9c22e50.png)
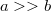 , mekkora a kölcsönös induktivitás?
, mekkora a kölcsönös induktivitás? ![\[L=\dfrac{\Phi}{I}=\dfrac{\mu_0 \pi b^2 }{2 a}\]](/images/math/7/1/1/7116234d52cea64595b8ec4ec1c9e492.png)
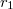 és
és 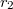 sugarú koaxiális hengerpár közti teret két különböző
sugarú koaxiális hengerpár közti teret két különböző 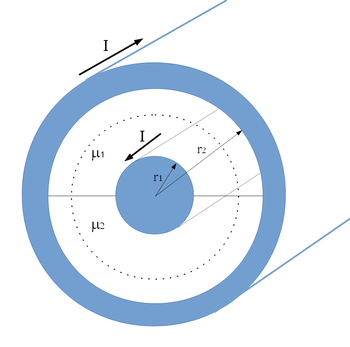
![\[L= \dfrac{\mu_0 \mu_1 \mu_2}{\pi(\mu_1+\mu_2)} ln \dfrac{r_{2}}{r_{1}}\]](/images/math/0/e/a/0eac5c7dd6c9b225f1bd78907c098d13.png)
![\[ \mu_v=\dfrac{2\pi r-d}{\dfrac{NI\mu_0}{B}-d}\]](/images/math/e/f/6/ef676285e4e96f85f1f0a3f9c104cd30.png)
 szélességű,
szélességű, 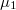 a másik felét
a másik felét 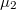 relatív mágneses permeabilitású anyag tölti ki? Tételezzük fel, hogy
relatív mágneses permeabilitású anyag tölti ki? Tételezzük fel, hogy 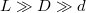
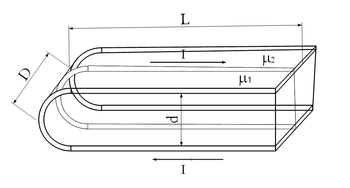
![\[ L=\dfrac{ 2ld \mu_1 \mu_2}{D(\mu_1+\mu_2)}\]](/images/math/3/b/9/3b927ac8777405a6971887687dfb2291.png)