„Elektrosztatika példák - Töltésen végzett munka” változatai közötti eltérés
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 2. Kategória:Szerkesztő:Beleznai Kategória:Elektrosztatika {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
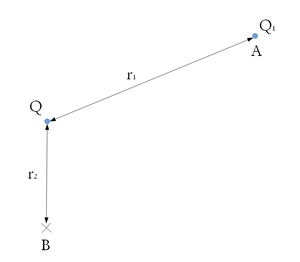
| − | </noinclude><wlatex>#Mekkora munkát kell végeznünk, ha a $Q_1$ töltést az ábrán látható $Q$ töltés környezetében az $A$ pontból a $B$ pontba visszük át? | + | </noinclude><wlatex>#Mekkora munkát kell végeznünk, ha a $Q_1$ töltést az ábrán látható $Q$ töltés környezetében az $A$ pontból a $B$ pontba visszük át? [[Kép:KFGY2-2-3.png|none|300px]] |
</wlatex><includeonly><wlatex>{{Útmutatás|content=Először mozgassuk a $Q_1$ ponttöltést az $r1$ sugarú, $Q$ középpontú köríven, ezt követően a $Q_1$ töltést sugárirányban mozgatjuk a $B$ pontig.}}{{Végeredmény|content=$$W=-\dfrac{Q_1}{4\pi\varepsilon_0}\int_{r1}^{r2}\dfrac{1}{r^2}dr=-\dfrac{Q_1}{4\pi\varepsilon_0}\left( \dfrac{1}{r1}-\dfrac{1}{r2} \right)$$}} | </wlatex><includeonly><wlatex>{{Útmutatás|content=Először mozgassuk a $Q_1$ ponttöltést az $r1$ sugarú, $Q$ középpontú köríven, ezt követően a $Q_1$ töltést sugárirányban mozgatjuk a $B$ pontig.}}{{Végeredmény|content=$$W=-\dfrac{Q_1}{4\pi\varepsilon_0}\int_{r1}^{r2}\dfrac{1}{r^2}dr=-\dfrac{Q_1}{4\pi\varepsilon_0}\left( \dfrac{1}{r1}-\dfrac{1}{r2} \right)$$}} | ||
</wlatex></includeonly><noinclude> | </wlatex></includeonly><noinclude> | ||
A lap 2013. július 28., 11:13-kori változata
Feladat
- Mekkora munkát kell végeznünk, ha a
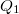töltést az ábrán látható 
töltés környezetében az 
pontból a 
pontba visszük át? 
Megoldás
Először mozgassuk a 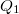ponttöltést az 
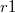sugarú, középpontú köríven addig, amíg a , a és a 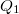ponttöltés egy egyenesre nem esik. Ezen a köríven mozogva a 
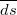elemi elmozdulások mindvégig merőlegesek a töltés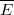 
elektromos terére, így a mozgatáskor nem történik munkavégzés.
Ezt követően a 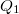töltést sugárirányban mozgatjuk a pontig. Ezen út során a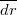 
elemi elmozdulások mindvégig merőlegesek a töltés 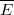elektromos terére, így az általunk végzett munka:
![\[W=-Q_1\int_{r1}^{r2}\overline{Edr}=-Q_1\int_{r1}^{r2}Edr\]](/images/math/6/1/c/61c85a935d54fbedda208d346ccbedfa.png)
ahol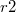 
a pont -tól mért távolsága. A negatív előjelre azért van szükség, mert az elektromos tér által kifejtett erő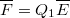 
. A 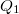töltés mozgatásához viszont ezzel ellentétes irányú, megegyező nagyságú 
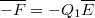erőre van szükség.
A feladat pedig nem a tér munkájára, hanem a testet mozgató erő munkájára kíváncsi.
A ponttöltés terét az integrálba behelyettesítve megkapjuk a végzett munkát:
![\[W=-\dfrac{Q_1}{4\pi\varepsilon_0}\int_{r1}^{r2}\dfrac{1}{r^2}dr=-\dfrac{Q_1}{4\pi\varepsilon_0}\left( \dfrac{1}{r1}-\dfrac{1}{r2} \right)\]](/images/math/8/3/6/8364d4d6f8d43af95efb89114bcf36d8.png)
