„Magnetosztatika példák - Négyzetes keresztmetszetű toroid forgástengelyében hosszú egyenes vezetővel” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 2. Kategória:Szerkesztő:Beleznai Kategória:Magnetosztatika {{Kísérleti fizika gyakorlat | tárgynév …”) |
(→Megoldás) |
||
| 14. sor: | 14. sor: | ||
Folyjon $I$ áram a végtelen hosszú egyenes vezetőben. Ennek mágneses terét a hely függvényében könnyen meghatározhatjuk az Amper-féle gerjesztési törvény segítségével: | Folyjon $I$ áram a végtelen hosszú egyenes vezetőben. Ennek mágneses terét a hely függvényében könnyen meghatározhatjuk az Amper-féle gerjesztési törvény segítségével: | ||
| − | $$ | + | $$B(r)=\dfrac{\mu_0 I}{2\pi r}$$ |
| − | Határozzuk meg a végtelen vezető által keltett $ | + | Határozzuk meg a végtelen vezető által keltett $B(r)$ mágneses indukció toroid négyzetes keresztmetszete által határolt fluxusát: |
| − | $$\phi=\int{}BdA=a\int_{d}^{d+a} | + | $$\phi=\int{}BdA=a\int_{d}^{d+a}B(r)dr=\dfrac{\mu_0 aI}{2\pi}\int_{d}^{d+a}\dfrac{1}{r}dr=\dfrac{\mu_0 aI}{2\pi} ln \left( \dfrac{d+a}{d} \right)$$ |
Ez alapján a kölcsönös indukció könnyen számítható, ha tudjuk, hogy a fent kiszámított fluxust a tekercs $N$-szer kerüli meg: | Ez alapján a kölcsönös indukció könnyen számítható, ha tudjuk, hogy a fent kiszámított fluxust a tekercs $N$-szer kerüli meg: | ||
A lap jelenlegi, 2013. október 1., 08:31-kori változata
Feladat
- Egy
menetszámú, 
belső sugarú, 
oldalhosszúságú négyzetes keresztmetszetű toroid forgástengelyében hosszú egyenes vezető helyezkedik el. Mekkora a rendszer kölcsönös induktivitása?
Megoldás
Folyjon 
áram a végtelen hosszú egyenes vezetőben. Ennek mágneses terét a hely függvényében könnyen meghatározhatjuk az Amper-féle gerjesztési törvény segítségével:
![\[B(r)=\dfrac{\mu_0 I}{2\pi r}\]](/images/math/b/a/6/ba69b7d72e28629fdac5484cb08aa433.png)
Határozzuk meg a végtelen vezető által keltett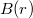 
mágneses indukció toroid négyzetes keresztmetszete által határolt fluxusát:
![\[\phi=\int{}BdA=a\int_{d}^{d+a}B(r)dr=\dfrac{\mu_0 aI}{2\pi}\int_{d}^{d+a}\dfrac{1}{r}dr=\dfrac{\mu_0 aI}{2\pi} ln \left( \dfrac{d+a}{d} \right)\]](/images/math/a/2/1/a2140a1f91dd566d59bace5ad7351fa7.png)
Ez alapján a kölcsönös indukció könnyen számítható, ha tudjuk, hogy a fent kiszámított fluxust a tekercs -szer kerüli meg:
![\[L=\dfrac{N\Phi}{I}=\dfrac{\mu_0 Na}{2\pi} ln \left( \dfrac{d+a}{d} \right)\]](/images/math/9/4/b/94b016c2f7fd9515af770862d9c22e50.png)
