„Mechanika - Energia húrdarabban” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
(→Feladat) |
||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (7.29.) Számítsuk ki, hogy mekkora energia van egy húr $80\,\rm g$-os részében (feltételezzük, hogy ez a rész sokkal rövidebb a hullámhossznál), ha a húrban $A=0,160\,\rm{mm}$ amplitúdójú és $f=120\,\rm{Hz}-es hullám terjed!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$E=0,58\,\rm{mJ}$$}}</wlatex></includeonly><noinclude> | + | </noinclude><wlatex># (7.29.) Számítsuk ki, hogy mekkora energia van egy húr $80\,\rm g$-os részében (feltételezzük, hogy ez a rész sokkal rövidebb a hullámhossznál), ha a húrban $A=0,160\,\rm{mm}$ amplitúdójú és $f=120\,\rm{Hz}$-es hullám terjed!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$E=0,58\,\rm{mJ}$$}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>Mivel a kiszemelt rész $l$ hosszára $l\ll\lambda$, minden pontja azonos fázisban rezgőnek tekinthető. A hullám energiája ebben a részben megegyezik a maximális mozgási energiával, tehát $$E=\frac12m(\omega A)^2=0,58\,\rm{mJ}$$</wlatex> | <wlatex>Mivel a kiszemelt rész $l$ hosszára $l\ll\lambda$, minden pontja azonos fázisban rezgőnek tekinthető. A hullám energiája ebben a részben megegyezik a maximális mozgási energiával, tehát $$E=\frac12m(\omega A)^2=0,58\,\rm{mJ}$$</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. február 23., 20:38-kori változata
Feladat
- (7.29.) Számítsuk ki, hogy mekkora energia van egy húr
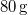-os részében (feltételezzük, hogy ez a rész sokkal rövidebb a hullámhossznál), ha a húrban 
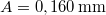amplitúdójú és 
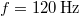-es hullám terjed!
Megoldás
Mivel a kiszemelt rész
hosszára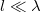 
, minden pontja azonos fázisban rezgőnek tekinthető. A hullám energiája ebben a részben megegyezik a maximális mozgási energiával, tehát ![\[E=\frac12m(\omega A)^2=0,58\,\rm{mJ}\]](/images/math/d/e/6/de67a4a8d1ebb70b1fce8b391d3bfd0d.png)
