Magnetosztatika - Mágneses térerősség. Kölcsönös és öninduktivitás
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Beleznai (vitalap | szerkesztései) 2013. július 15., 16:33-kor történt szerkesztése után volt.
Feladatok
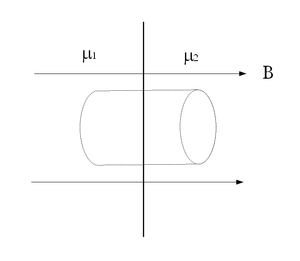
- A mágneses indukció
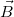 vektorára merőleges sík
vektorára merőleges sík 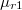 és
és 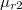 relatív permeabilitású anyagokat választ el egymástól. Tekintsünk egy hengert, melynek
relatív permeabilitású anyagokat választ el egymástól. Tekintsünk egy hengert, melynek  területű körlapjai párhuzamosak a határfelülettel! Határozzuk meg a
területű körlapjai párhuzamosak a határfelülettel! Határozzuk meg a 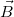 mágneses indukció és a
mágneses indukció és a 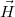 mágneses térerősség fluxusát erre a hengerre!ÚtmutatásÍrjuk fel a két térrészben
mágneses térerősség fluxusát erre a hengerre!ÚtmutatásÍrjuk fel a két térrészben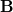 és
és 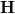 értékét a határfeltétel szerint, és vizsgáljuk meg, mi ad járulékot a fluxus integráljában! Végeredmény
értékét a határfeltétel szerint, és vizsgáljuk meg, mi ad járulékot a fluxus integráljában! Végeredmény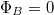
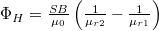
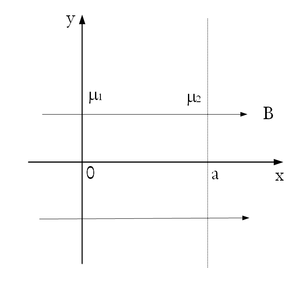
- Végtelen kiterjedésű,
 vastagságú lemez az 1. ábrának megfelelően
vastagságú lemez az 1. ábrának megfelelően  irányú,
irányú,  indukciójú térben helyezkedik el. A lemez anyagának relatív permeabilitása balról jobbra lineárisan változik
indukciójú térben helyezkedik el. A lemez anyagának relatív permeabilitása balról jobbra lineárisan változik 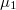 -ről
-ről 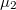 -re.
-re.
a) Határozzuk meg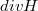 -t
-t  függvényében!
függvényében!
b) Mekkora a térerősség fluxusa egy
térerősség fluxusa egy  tengelyű hengerre, amelynek
tengelyű hengerre, amelynek  területű alap és fedőköre
területű alap és fedőköre 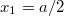 és
és 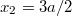 helyen van?
helyen van?
Végeredménya)![\[divH=\dfrac{dH}{dx}=-\dfrac{\dfrac{B(\mu_2-\mu_1)}{a\mu_0}}{\left( \mu_1+\dfrac{x}{a}(\mu_2-\mu_1)\right)^2}\]](/images/math/1/7/b/17be334635fbcaf47f513b258253ff31.png)
b)![\[\Phi=\dfrac{SB}{\mu_0}\left( \dfrac{2}{\mu_1+\mu_2} -1\right)\]](/images/math/3/d/c/3dc544ecb6e9149678e1dd4081554882.png)
 sugarú toroid
sugarú toroid  menetében
menetében  erősségű áram folyik. A toroid
erősségű áram folyik. A toroid  sugarú belsejét
sugarú belsejét 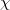 mágneses szuszceptibilitású anyag tölti ki.
mágneses szuszceptibilitású anyag tölti ki.
a) Mekkora a mágneses térerősség?
b) Mekkora a mágnesezettség?
c) Mekkora a mágneses indukció?Végeredménya)![\[H=\dfrac{NI}{2\pi R}\]](/images/math/e/f/7/ef7b021524d2766df430c52081ff17ff.png)
b)![\[M=\dfrac{\chi NI}{2\pi R}\]](/images/math/7/2/4/724d3ebed60d8e2d94a56adf2db2b72c.png)
c)![\[B=\dfrac{\mu_0(1+\chi)NI}{2\pi R}\]](/images/math/6/4/d/64d6c1a3711974ae534095ccd93b3624.png)
- Egy
 hosszúságú,
hosszúságú,  sugarú,
sugarú,  menetű szolenoidban
menetű szolenoidban  erősségű áram folyik. A szolenoidba helyezünk egy ugyanolyan keresztmetszetű,
erősségű áram folyik. A szolenoidba helyezünk egy ugyanolyan keresztmetszetű, 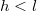 hosszúságú vashengert, amelynek relatív permeabilitása
hosszúságú vashengert, amelynek relatív permeabilitása 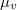 . Számítsuk ki a mágneses térerősség és a mágneses indukció értékét a vason belül és kívül! Végeredmény
. Számítsuk ki a mágneses térerősség és a mágneses indukció értékét a vason belül és kívül! Végeredmény![\[H_{vas}=\dfrac{ NI}{h\left( 1-\mu_v \right)+l\mu_v} \]](/images/math/6/7/3/6730cbd97b876de3ebcccca9f4c977c1.png)
![\[H_{levego}=\dfrac{ NI}{h\left( \dfrac{1}{\mu_v}-1 \right)+l} \]](/images/math/b/0/d/b0d5b84ff5d21a562d4319522ce4bcb1.png)
- Egy
 hosszúságú,
hosszúságú,  sugarú,
sugarú,  menetű szolenoidban
menetű szolenoidban  erősségű áram folyik. A szolenoidba helyezünk egy ugyanolyan hosszúságú, de
erősségű áram folyik. A szolenoidba helyezünk egy ugyanolyan hosszúságú, de 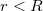 sugarú vashengert, amelynek relatív permeabilitása
sugarú vashengert, amelynek relatív permeabilitása 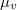 . Számítsuk ki a tekercs indukciófluxusát! Végeredmény
. Számítsuk ki a tekercs indukciófluxusát! Végeredmény![\[ \Phi=A_{vas}B_{vas}+A_{levego}B_{levego}=\dfrac{NI\mu_0\pi}{l} \left( R^2+r^2(\mu_v-1)\right)\]](/images/math/2/5/0/2509298a9e4d235a7e8a9dffede56072.png)
- Határozzuk meg egy
 árammal átjárt,
árammal átjárt,  menetű,
menetű,  hosszúságú,
hosszúságú,  keresztmetszetű szolenoid fluxusát és öninduktivitását!Végeredmény
keresztmetszetű szolenoid fluxusát és öninduktivitását!Végeredmény![\[L=\dfrac{N\Phi}{I}=\dfrac{\mu_0 N^2 A}{l}\]](/images/math/8/e/5/8e54a8ed946b42adec93779cfe4cf850.png)
- Egy
 hosszúságú koaxiális hengerpár belső,
hosszúságú koaxiális hengerpár belső, 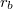 sugarú hengerfelületen
sugarú hengerfelületen  áram folyik a tengely irányában, míg a külső,
áram folyik a tengely irányában, míg a külső, 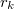 sugarú felületen ugyanakkora, de ellentétes irányú áram folyik. Számítsuk ki a rendszer öninduktivitását! Végeredmény
sugarú felületen ugyanakkora, de ellentétes irányú áram folyik. Számítsuk ki a rendszer öninduktivitását! Végeredmény![\[L=\dfrac{\Phi}{I}=\dfrac{\mu_0 l}{2\pi}ln\left( \dfrac{r_k}{r_b} \right)\]](/images/math/2/9/7/297098928cbccf0502612f516f6e4011.png)
- Mekkora a fluxus (homogén árameloszlás esetén) egy
 sugarú tömör hengeres vezető (relatív permeabilitása
sugarú tömör hengeres vezető (relatív permeabilitása 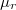 )
)  hosszúságú darabjában? Mekkora öninduktivitást kölcsönöz a vezetéknek a henger belsejében kialakult mágneses tér? Végeredmény
hosszúságú darabjában? Mekkora öninduktivitást kölcsönöz a vezetéknek a henger belsejében kialakult mágneses tér? Végeredmény![\[\Phi=\dfrac{\mu_0 l I}{4\pi}\]](/images/math/9/f/c/9fcde8b3bcbd4214a337f80155023f86.png)
![\[L=\dfrac{\Phi}{I}=\dfrac{\mu_0 l}{4\pi}\]](/images/math/7/2/1/72118da80c69bc079f976d8be6a8a6fe.png)
- Határozzuk meg egy
 oldalú, négyzet keresztmetszetű,
oldalú, négyzet keresztmetszetű,  menetű toroid tekercs öninduktivitását, ha a tekercs belső sugara
menetű toroid tekercs öninduktivitását, ha a tekercs belső sugara  !ÚtmutatásHatározzuk meg a
!ÚtmutatásHatározzuk meg a mágneses térerősséget a tekercs belsejében a tengelytől mért távolság függvényében a gerjesztési törvénysegítségével, számoljuk ki ebből 1 menetre a fluxust, végül az
mágneses térerősséget a tekercs belsejében a tengelytől mért távolság függvényében a gerjesztési törvénysegítségével, számoljuk ki ebből 1 menetre a fluxust, végül az  menet fluxusából határozzuk meg az önindukciós együtthatót! Végeredmény
menet fluxusából határozzuk meg az önindukciós együtthatót! Végeredmény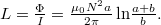
- Mekkora az öninduktivitása két igen hosszú, párhuzamos,
 sugarú hengerből álló vezetőpár
sugarú hengerből álló vezetőpár  hosszúságú darabjának, ha a vezetékek
hosszúságú darabjának, ha a vezetékek  távolságra vannak egymástól? Végeredmény
távolságra vannak egymástól? Végeredmény![\[L=L_1+2L_2=\dfrac{\mu_0 l}{\pi} ln \left( \dfrac{d-R}{R} \right)+\dfrac{\mu_0 l}{2\pi}\]](/images/math/2/7/9/2796ef6098223b4acf0bffa730b93b79.png)
- Egy
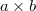 oldalhosszúságú, téglalap alakú vezető keret síkjában az
oldalhosszúságú, téglalap alakú vezető keret síkjában az  oldalú éllel párhuzamosan, attól
oldalú éllel párhuzamosan, attól  távolságra elhelyezünk egy végtelen hosszúnak tekinthető egyenes vezetőt. Mekkora az egyenes vezető és a vezető keret közti kölcsönös induktivitás? Végeredmény
távolságra elhelyezünk egy végtelen hosszúnak tekinthető egyenes vezetőt. Mekkora az egyenes vezető és a vezető keret közti kölcsönös induktivitás? Végeredmény![\[L=L_1+2L_2=\dfrac{\mu_0 l}{\pi} ln \left( \dfrac{d-R}{R} \right)+\dfrac{\mu_0 l}{2\pi}\]](/images/math/2/7/9/2796ef6098223b4acf0bffa730b93b79.png)
- Egy
 menetszámú,
menetszámú,  belső sugarú,
belső sugarú,  oldalhosszúságú négyzetes keresztmetszetű toroid forgástengelyében hosszú egyenes vezető helyezkedik el. Mekkora a rendszer kölcsönös induktivitása? Végeredmény
oldalhosszúságú négyzetes keresztmetszetű toroid forgástengelyében hosszú egyenes vezető helyezkedik el. Mekkora a rendszer kölcsönös induktivitása? Végeredmény![\[L=\dfrac{N\Phi}{I}=\dfrac{\mu_0 Na}{2\pi} ln \left( \dfrac{d+a}{d} \right)\]](/images/math/9/4/b/94b016c2f7fd9515af770862d9c22e50.png)
 sugarú körvezetővel azonos síkban koncentrikusan helyezkedik el egy
sugarú körvezetővel azonos síkban koncentrikusan helyezkedik el egy  sugarú körvezető. Feltéve, hogy
sugarú körvezető. Feltéve, hogy 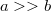 , mekkora a kölcsönös induktivitás? Végeredmény
, mekkora a kölcsönös induktivitás? Végeredmény![\[L=\dfrac{\Phi}{I}=\dfrac{\mu_0 \pi b^2 }{2 a}\]](/images/math/7/1/1/7116234d52cea64595b8ec4ec1c9e492.png)
- Egy
 hosszúságú,
hosszúságú, 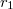 és
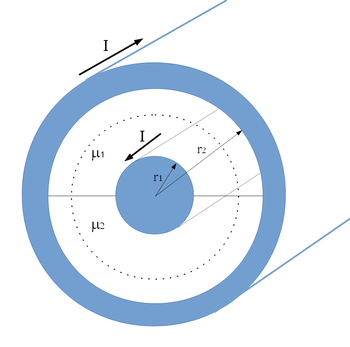
és 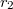 sugarú koaxiális hengerpár közti teret két különböző
sugarú koaxiális hengerpár közti teret két különböző 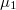 és
és 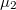 relatív mágneses permeabilitású anyag tölti ki az 1. ábra szerint. A hengerpaláston ellentétes irányban, a tengellyel párhuzamosan folyik
relatív mágneses permeabilitású anyag tölti ki az 1. ábra szerint. A hengerpaláston ellentétes irányban, a tengellyel párhuzamosan folyik  felületi áram. Az áram a belső henger külső felületén folyik, a külső henger vastagságát pedig elhanyagolhatjuk. Mekkora a rendszer öninduktivitása?
felületi áram. Az áram a belső henger külső felületén folyik, a külső henger vastagságát pedig elhanyagolhatjuk. Mekkora a rendszer öninduktivitása?
Végeredmény![\[L= \dfrac{\mu_0 \mu_1 \mu_2}{\pi(\mu_1+\mu_2)} ln \dfrac{r_{2}}{r_{1}}\]](/images/math/0/e/a/0eac5c7dd6c9b225f1bd78907c098d13.png)
- Egy
 sugarú toroid tekercs vasmagján kicsiny
sugarú toroid tekercs vasmagján kicsiny  vastagságú légrés található. A tekercs menetszáma
vastagságú légrés található. A tekercs menetszáma  , benne
, benne  áramerősség folyik. A légrésben
áramerősség folyik. A légrésben  indukciójú mágneses tér mérhető. Mekkora a vasmag mágneses permeabilitása? Végeredmény
indukciójú mágneses tér mérhető. Mekkora a vasmag mágneses permeabilitása? Végeredmény![\[ \mu_v=\dfrac{2\pi r-d}{\dfrac{NI\mu_0}{B}-d}\]](/images/math/e/f/6/ef676285e4e96f85f1f0a3f9c104cd30.png)
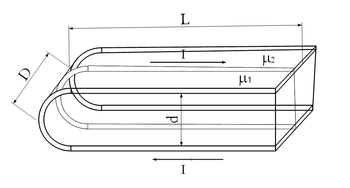
- Mekkora az öninduktivitása az 1. ábrán vázolt
 szélességű,
szélességű,  hosszúságú, egymástól
hosszúságú, egymástól  távolságra levő szalagpárnak, ha a szalagok közötti tér egyik felét
távolságra levő szalagpárnak, ha a szalagok közötti tér egyik felét 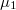 a másik felét
a másik felét 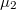 relatív mágneses permeabilitású anyag tölti ki? Tételezzük fel, hogy
relatív mágneses permeabilitású anyag tölti ki? Tételezzük fel, hogy 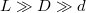
Végeredmény![\[ L=\dfrac{ 2ld \mu_1 \mu_2}{D(\mu_1+\mu_2)}\]](/images/math/3/b/9/3b927ac8777405a6971887687dfb2291.png)