Mechanika - Relativisztikus Doppler mechanikai hullámra
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2013. december 10., 12:18-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Hullámok |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (**7.8.) Egy
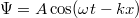 alakú rugalmas síkhullám
alakú rugalmas síkhullám 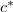 sebességgel terjed a
sebességgel terjed a  közegben. Határozzuk meg ennek a hullámnak a matematikai alakját abban a
közegben. Határozzuk meg ennek a hullámnak a matematikai alakját abban a 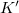 rendszerben, amely az
rendszerben, amely az  tengely irányában a
tengely irányában a  közeghez képest
közeghez képest  sebességgel halad, mind nem-relativisztikus, mind relativisztikus esetben!
sebességgel halad, mind nem-relativisztikus, mind relativisztikus esetben!
Megoldás
Nem-relativisztikus esetben a koordináta-transzformációk![\[t=t'\]](/images/math/8/c/3/8c364f3d4c24e870cbb933b378d0035a.png)
![\[x=x'+vt\]](/images/math/2/9/1/291a14e8cc01f65436556699f9964e93.png)
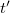 -vel és
-vel és 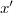 -vel arányos tényezőkből az alábbiak leolvashatók le:
-vel arányos tényezőkből az alábbiak leolvashatók le: ![\[k'=k\]](/images/math/a/1/2/a1284c1fdb214ac69558acacac071fc0.png)
![\[\omega'=\omega-vk,\]](/images/math/0/7/3/073b752ff2de8213f52e46d4a3bc7172.png)
![\[f'=f\left(\frac{c^*-v}{c^*}\right)=f\left(1-\frac v{c^*}\right),\]](/images/math/5/9/0/590b92b93a06b9348f21b235aba56335.png)
![\[(c^*)'=c^*-v\]](/images/math/3/9/4/394a065e5d0ea67812325bad1c7e47c0.png)
![\[x=\frac{x'+vt'}{\sqrt{1-\frac{v^2}{c^2}}}\]](/images/math/7/f/a/7fad83e12f308dcd123f67125980574d.png)
![\[t=\frac{t'+\frac v{c^2}x'}{\sqrt{1-\frac{v^2}{c^2}}},\]](/images/math/5/5/0/550e5bd4b49786bfe09e334719482508.png)
 a fénysebesség. Ezeket beírva a hullámfüggvény argumentumába a
a fénysebesség. Ezeket beírva a hullámfüggvény argumentumába a 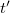 -vel és
-vel és 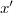 -vel arányos tényezőkből az alábbiak leolvashatók le:
-vel arányos tényezőkből az alábbiak leolvashatók le: ![\[k'=\frac{k-\frac v{c^2}\omega}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{k(1-\frac{vc^*}{c^2})}{\sqrt{1-\frac{v^2}{c^2}}}\]](/images/math/0/5/e/05eccbe154e6daf724371d0f71f282d7.png)
![\[\omega'=\frac{\omega-kv}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{\omega(1-\frac v{c^*})}{\sqrt{1-\frac{v^2}{c^2}}},\]](/images/math/5/b/9/5b95e43ae554f592a107bcc857bdc386.png)
![\[(c^*)'=\frac{\omega'}{k'}=\frac{\omega(1-v/c^*)}{k(1-vc^*/c^2)}=c^*\frac{1-v/c^*}{1-vc^*/c^2}=\frac{c^*-v}{1-\frac{vc^*}{c^2}},\]](/images/math/5/2/0/520d6e7999bba83f842a70f6a54fdcc4.png)
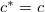 esetben visszakapjuk az elektromágneses hullámokra érvényes Doppler-képleteket. Ha a forrásnak is megengedtünk volna mozgást, akkor még bonyolultabb relativisztikus összefüggés kapható rugalmas hullámokra. Ez kis sebességek esetén visszaadja a nem-relativisztikus összefüggést, másrészt
esetben visszakapjuk az elektromágneses hullámokra érvényes Doppler-képleteket. Ha a forrásnak is megengedtünk volna mozgást, akkor még bonyolultabb relativisztikus összefüggés kapható rugalmas hullámokra. Ez kis sebességek esetén visszaadja a nem-relativisztikus összefüggést, másrészt 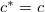 esetben úgy alakul át, hogy csak a forrás és a megfigyelő relatív sebessége számít, ha azt a relativisztikus sebességöszeadás szerint határozzuk meg.
esetben úgy alakul át, hogy csak a forrás és a megfigyelő relatív sebessége számít, ha azt a relativisztikus sebességöszeadás szerint határozzuk meg.
(Bővebben: http://mathpages.com/rr/s2-04/2-04.htm)