Elektrosztatika példák - Párhuzamos végtelen síklapok potenciáltere
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Beleznai (vitalap | szerkesztései) 2013. április 28., 16:17-kor történt szerkesztése után volt.
Feladat
- Két párhuzamos, nagy kiterjedésű vezető sík egyike földelt, a másik felületi töltéssűrűsége
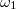 . A lemezek távolsága
. A lemezek távolsága  .
.
a) Mekkora a lemezek közötti potenciálkülönbség?
b) Mekkora lesz a potenciálkülönbség, ha a lemezekkel párhuzamosan, tőlük egyenlő távolságra, egy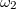 felületi töltéssűrűségű harmadik lemezt helyezünk?
felületi töltéssűrűségű harmadik lemezt helyezünk?
Megoldás
a) A földelt lemezen 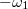 felületi töltéssűrűség alakul ki. A lemezek közötti térerősség:
felületi töltéssűrűség alakul ki. A lemezek közötti térerősség:
![\[\vec{E}=\frac{\omega_{1}}{\epsilon_{0}}\]](/images/math/b/c/9/bc90d1f978cbca8c4b854eb85a3b06ef.png)
Ebből a lemezek közötti potenciálkülönbség:
![\[ U =\frac{\omega_{1}}{\epsilon_{0}}\cdot d \]](/images/math/c/7/9/c7966653df23b09877d552d1a8120db2.png)
b)
Ebben az esetben a földelt lemezen kialakuló felületi töltéssűrűség: 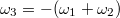 hiszen a földelt lemez helyén, a másik két lemez által okozott térerősség húzza fel a töltéseket a földből.Ebből a térerősségek a lemezek között:
hiszen a földelt lemez helyén, a másik két lemez által okozott térerősség húzza fel a töltéseket a földből.Ebből a térerősségek a lemezek között:
![\[\vec{E_{1}}=\frac{\omega_{1}}{2\cdot\epsilon_{0}}+\frac{\omega_{2}}{2\cdot\epsilon_{0}}-\frac{\omega_{3}}{2\cdot\epsilon_{0}}=\frac{\omega_{1}+\omega_{2}}{2\cdot\epsilon_{0}}\]](/images/math/e/3/d/e3d6752616ec40f24d46a0dba93c4c99.png)
![\[\vec{E_{2}}=\frac{\omega_{1}}{2\cdot\epsilon_{0}}-\frac{\omega_{2}}{2\cdot\epsilon_{0}}-\frac{\omega_{3}}{2\cdot\epsilon_{0}}=\frac{\omega_{1}}{\epsilon_{0}}\]](/images/math/2/1/0/21089ce7d9d5c7e0f7a891f808157e6b.png)
Ebből a potenciál különbség:
![\[U = U_{1}+U_{2} = \frac{\omega_{1}+\omega_{2}}{2\cdot\epsilon_{0}}\cdot d + \frac{\omega_{1}}{\epsilon_{0}}\cdot d = \frac{2\cdot\omega_{1}+\omega_{2}}{\epsilon_{0}}\cdot \frac{d}{2} \]](/images/math/6/b/0/6b05539342a4baf3ef56a0b244911a06.png)