Magnetosztatika példák - Koncentrikus körvezetők öninduktivitása
Feladat
 sugarú körvezetővel azonos síkban koncentrikusan helyezkedik el egy
sugarú körvezetővel azonos síkban koncentrikusan helyezkedik el egy  sugarú körvezető. Feltéve, hogy
sugarú körvezető. Feltéve, hogy 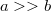 , mekkora a kölcsönös induktivitás?
, mekkora a kölcsönös induktivitás?
Megoldás
Folyjon  áram a nagyobbik,
áram a nagyobbik,  sugarú hurokban. Ennek mágneses tere a kör középpontjában kiszámítható a Biot-Savart törvény segítségével. Először együnk egy
sugarú hurokban. Ennek mágneses tere a kör középpontjában kiszámítható a Biot-Savart törvény segítségével. Először együnk egy  hosszúságú ívdarabot, melynek hosszát a hozzá tartozó infinitezimális középponti szög segítségével fejezünk ki:
hosszúságú ívdarabot, melynek hosszát a hozzá tartozó infinitezimális középponti szög segítségével fejezünk ki:
![\[dl=ad\varphi\]](/images/math/4/3/f/43fee0672bb03b68629683f368080512.png)
Ezen ívdarab által a kör középpontjában keltett 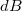 indukció járuléka a Biot-Savart törvény alapján a következő, kihasználva azt a tényt, hogy az érintő irányú ívdarab merőleges a kör sugarára:
indukció járuléka a Biot-Savart törvény alapján a következő, kihasználva azt a tényt, hogy az érintő irányú ívdarab merőleges a kör sugarára:
![\[dB=\dfrac{\mu_0 I}{4\pi}\dfrac{dl}{a^2}=\dfrac{\mu_0 I}{4\pi}\dfrac{d\varphi}{a}\]](/images/math/c/9/9/c9993ce9eefbf12cf192621e1d50f6f4.png)
Tudván, hogy a körív infinitezimális elemei által a középpontban keltett indukció járulékok iránya merőleges a kör síkjára, a teljes körív által keltett  indukciót egyszerűen kiszámíthatjuk:
indukciót egyszerűen kiszámíthatjuk:
![\[B=\int{}dB=\dfrac{\mu_0 I}{4\pi a}\int_{0}^{2pi}d\varphi=\dfrac{\mu_0 I}{4\pi a}2\pi=\dfrac{\mu_0 I}{2 a}\]](/images/math/a/8/0/a8061bc64f704fda1457ddd2d8b67e41.png)
Ezután feltételezzük, hogy a nagyobbik gyűrű középpontja körüli kicsiny  sugarú környezetben a mágneses indukció homogén. Így a
sugarú környezetben a mágneses indukció homogén. Így a  sugarú gyűrű által körülzárt mágneses tér fluxusa:
sugarú gyűrű által körülzárt mágneses tér fluxusa:
![\[\Phi=b^2\pi B=\dfrac{\mu_0 \pi b^2 I }{2 a}\]](/images/math/d/4/f/d4fa7bd82cd19af01a1e61b6d91361f8.png)
A kölcsönös indukció tehát:
![\[L=\dfrac{\Phi}{I}=\dfrac{\mu_0 \pi b^2 }{2 a}\]](/images/math/7/1/1/7116234d52cea64595b8ec4ec1c9e492.png)