Magnetosztatika példák - Párhuzamos henger alakú vezetőpár öninduktivitása
Feladat
- Mekkora az öninduktivitása két igen hosszú, párhuzamos,
sugarú hengerből álló vezetőpár 
hosszúságú darabjának, ha a vezetékek 
távolságra vannak egymástól?
Megoldás
Az egyik hengeres vezetőben folyjon 
áram a vezető tengelye mentén, míg a másik hengerben folyjon ugyanakkora, de ellentétes irányú áram. Az önindukció számításához szükség lesz az 1. ábrán besatírozott terület fluxusára.
Egy áram által átjárt vezeték tere az Amper-féle gerjesztési törvény segítségével könnyen kiszámítható:
![\[B_{(r)}=\dfrac{\mu_0 I}{2\pi r}\]](/images/math/e/1/9/e19d8fa41e8b66fef89e955cdafc2ca6.png)
Ennek fluxusa a két hosszúságú, sugarú henger által közrezárt területen:
![\[\phi=\int{}BdA=a\int_{R}^{d-R}B_{r}dr=\dfrac{\mu_0 lI}{2\pi}\int_{R}^{d-R}\dfrac{1}{r}dr=\dfrac{\mu_0 lI}{2\pi} ln \left( \dfrac{d-R}{R} \right)\]](/images/math/c/6/d/c6dbfb396691398d1851b16c0057031a.png)
Ezzel megkaptuk a két vezeték által határolt térben az egyik vezeték által keltett fluxust. A rendszer szimmetriája miatt a másik vezeték fluxusjáruléka szintén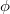 
. Könnyen belátható, hogy ezen két fluxusjárulék összeadódik, így az 1. ábrán satírozott terület összes fluxusa:
![\[\Phi=2\phi=\dfrac{\mu_0 lI}{\pi} ln \left( \dfrac{d-R}{R} \right)\]](/images/math/0/c/a/0cab791119b6baddfde5502600cf62f1.png)
Tehát a rendszer önindukciója:
![\[L_1=\dfrac{\Phi}{I}=\dfrac{\mu_0 l}{\pi} ln \left( \dfrac{d-R}{R} \right)\]](/images/math/5/6/9/5690d22e972256ed8a1dccc21fa0f770.png)
Megjegyzés: A fenti eredmény elhanyagolja a vezetékek belsejében mérhető mágneses tér önindukció-járulékát. A Tömör hengeres vezető öninduktivitása feladat megoldása alapján tudjuk, hogy egy hosszúságú, sugarú vezetékdarab belsejébe zárt tér által okozott önindukció:
![\[L_2=\dfrac{\mu_0 l}{4\pi}\]](/images/math/e/9/1/e91783a482fb98e675e4ad47829d04af.png)
Ennek felhasználásával a jelenlegi feladat eredményét pontosíthatjuk, ha a kapott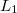 
eredményhez hozzáadjuk a két vezeték belsejének indukció járulékát.
![\[L=L_1+2L_2=\dfrac{\mu_0 l}{\pi} ln \left( \dfrac{d-R}{R} \right)+\dfrac{\mu_0 l}{2\pi}\]](/images/math/2/7/9/2796ef6098223b4acf0bffa730b93b79.png)
