Elektrosztatika példák - Vezető félgömb potenciálja a gömb középpontjában

Feladat

1. Egy $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú félgömbhéjat feltöltünk $\setbox0\hbox{$Q$}% \message{//depth:\the\dp0//}% \box0%$ töltéssel. Mekkora a potenciál a gömb középpontjában, a végtelen távol lévő ponthoz képest? A megoldáshoz használjuk a szuperpozíció elvét.

Megoldás

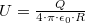Egy $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú gömb potenciálja $\setbox0\hbox{$U = \frac{Q}{4\cdot\pi\cdot\epsilon_{0}\cdot R}$}% \message{//depth:\the\dp0//}% \box0%$. A szuperpozíció elve miatt a gömb teljes potenciálja összege két félgömb potenciáljának, vagyis: $\setbox0\hbox{$U_{gomb} = U_{felgomb1}+U_{felgomb2}$}% \message{//depth:\the\dp0//}% \box0%$.

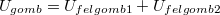Mivel a két félgömb pontenciálja azonos ( szimmetriai megfontolások alapján) ezért a sélgömb potenciálja:

$\[U_{felgomb} = \frac{U_{gomb}}{2} = \frac{Q}{8\cdot\pi\cdot\epsilon_{0}\cdot R}\]$