Magnetosztatika példák - Tömör hengeres vezető öninduktivitása

Feladat

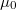1. Mekkora a fluxus (homogén árameloszlás esetén) egy $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú tömör hengeres vezető (relatív permeabilitása $\setbox0\hbox{$\mu_0$}% \message{//depth:\the\dp0//}% \box0%$) $\setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú darabjában? Mekkora öninduktivitást kölcsönöz a vezetéknek a henger belsejében kialakult mágneses tér?

Megoldás

Folyjon $\setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0%$ áram a vezetékben. Ekkor homogén árameloszlás esetén az áramsűrűség nagysága:

$\[j=\dfrac{I}{R^2\pi}\]$

Ennek ismeretében határozzuk meg a mágneses térerősséget a vezeték belsejében. Vegyünk fel egy 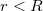$\setbox0\hbox{$r<R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú kört, melynek tengelye egybeesik a vezeték tengelyével. A felvett kör által határolt területen átfolyó áramerősség:

$\[I(r)=jr^2\pi=\dfrac{I}{R^2\pi}r^2\pi=I\dfrac{r^2}{R^2}\]$

Az áram ismeretében felírhatjuk a zárt görbére az Amper-féle gerjesztési törvényt:

$\[I(r)=\oint{}\vec{H(r)} \vec{dl}\]$

A rendszer hengerszimmetriája alapján a fenti egyenletet így is felírhatjuk:

$\[I\dfrac{r^2}{R^2}=2\pi r H(r)\]$

A mágneses tér nagyságának helyfügése a vezeték belsejében tehát:

$\[H(r)=\dfrac{I}{2\pi R^2}r\]$

A mágneses indukció pedig:

$\[B(r)=\dfrac{\mu_0 I}{2\pi R^2}r\]$

A mágneses indukció fluxusát kiszámíthatjuk az $\setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú vezetékdarab belsejében:

$\[\Phi=\int{}BdA=l\int_{0}^{R}B(r)dr=\dfrac{\mu_0 l I}{2\pi R^2}\int_{0}^{R}rdr=\dfrac{\mu_0 l I}{2\pi R^2} \dfrac{R^2}{2}=\dfrac{\mu_0 l I}{4\pi}\]$

A vezetékdarab belsejében levő tér okozta öninduktivitás:

$\[L=\dfrac{\Phi}{I}=\dfrac{\mu_0 l}{4\pi}\]$