Termodinamika példák - Dinamikus fűtés hőszivattyúval
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Stippinger (vitalap | szerkesztései) 2012. október 10., 12:12-kor történt szerkesztése után volt.
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Fajhő, Körfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy épület fűtésére az ún. dinamikus fűtést használjuk:
- A fűtőanyagot elégetjük egy hőerőgép tűzszekrényében, melynek hőmérsékletét állandó
 hőmérsékleten tartjuk (ez a hőerőgép felső hőtartálya).
hőmérsékleten tartjuk (ez a hőerőgép felső hőtartálya).
- A hőerőgép egy hőszivattyút működtet, amelynek alsó hőtartálya egy tó
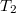 hőmérsékletű vize, felső hőtartálya pedig a hőerőgépet hűtő
hőmérsékletű vize, felső hőtartálya pedig a hőerőgépet hűtő  hőmérsékletű víz, amely az épületet egyúttal fűti (
hőmérsékletű víz, amely az épületet egyúttal fűti (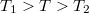 ).
).
- A tűzszekrényben
 égéshőjű anyag ég, a hőerőgép és a hőszivattyú veszteség nélkül Carnot--hatásfokkal működik. Határozzuk meg, mennyi hőt kap a helyiség egységnyi tömegű fűtőanyag elégetése árán!
égéshőjű anyag ég, a hőerőgép és a hőszivattyú veszteség nélkül Carnot--hatásfokkal működik. Határozzuk meg, mennyi hőt kap a helyiség egységnyi tömegű fűtőanyag elégetése árán!
- A fűtőanyagot elégetjük egy hőerőgép tűzszekrényében, melynek hőmérsékletét állandó
Megoldás
A 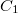 körfolyamat által termelt munka
körfolyamat által termelt munka
![\[W=Q_1-|Q_1'|,\]](/images/math/7/1/8/7186ffb7a53b17699180ae5defae5506.png)
a körfolyamat hatásfoka pedig
![\[\eta_1=\frac{W}{Q_1}=1-\frac{|Q_1'|}{Q_1}=1-\frac{T}{T_1}.\]](/images/math/3/1/a/31abc89a53b146ecfa7d5e455b9aee6f.png)
Kifejezve a lakásnak átadott 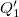 maradványhőt
maradványhőt
![\[|Q_1'|=Q_1\frac{T}{T_1}\]](/images/math/c/b/9/cb97abbd218d471f76bf3f73b93a35d2.png)
a munka kifejezése egyszerűsödik:
![\[W=Q_1\left(1-\frac{T}{T_1}\right).\]](/images/math/a/d/0/ad09bcb1679432e86a5ecfd18e6740f2.png)
Mivel a felső hőtartályt állandó hőmérsékletűnek tartjuk 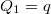 .
.
A 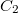 körfolyamat hatásfoka
körfolyamat hatásfoka
![\[\eta_2=\frac{W}{|Q_2'|}=1-\frac{T_2}{T}\]](/images/math/e/3/b/e3bf487a601ab124541c7ed0fd4fc1fa.png)
segítségével a fűtésre juttatott hő kifejezhető:
![\[|Q_2'|=\frac{W}{1-\frac{T_2}{T}}=Q_1\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}\]](/images/math/3/f/5/3f5af2e82aa78fc11a08fe138efcc6e9.png)
A teljes rendszer fűtőteljesítménye
![\[Q=|Q_1'|+|Q_2'|=Q_1\left(\frac{T}{T_1}+\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}\right)= Q_1\left(\frac{\frac{T}{T_1}-\frac{T_2}{T_1}}{1-\frac{T_2}{T}}+\frac{1-\frac{T}{T_1}}{1-\frac{T_2}{T}}\right)= Q_1\frac{1-\frac{T_2}{T_1}}{1-\frac{T_2}{T}}>q\]](/images/math/b/4/5/b4587542cf05fcba619cb8ce018998e3.png)
hiszen 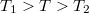 .
.
