Mechanika - Hullámok
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. december 29., 18:08-kor történt szerkesztése után volt.
Feladatok
- (7.1.) Mi a frekvenciája és terjedési sebessége az függvénnyel megadott hullámnak? (
![\[y=4\sin2\pi\left(\frac t{0,02}-\frac x4\right)\]](/images/math/3/4/3/34343bf1b77c4b2bade83dc0981fadbe.png)
 -t s-okban,
-t s-okban,  -et m-ekben mérjük.)Végeredmény
-et m-ekben mérjük.)Végeredmény![\[f=50\,\rm{Hz}\]](/images/math/e/d/0/ed0391d03e98bf23c8af1306ec400fa9.png)
![\[v=200\,\rm{\frac ms}\]](/images/math/c/a/c/cac595bb9c9beed4d801e6e87b6646e5.png)
- (S-Je8 16.18) Egy húron terjedő transzverzális szinuszos hullám periódusideje
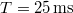 , és
, és 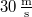 sebességgel halad
sebességgel halad  irányban. Az
irányban. Az 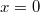 pont kitérése
pont kitérése  -ban
-ban 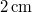 , sebessége
, sebessége 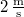 . Mekkora a hullám amplitúdója? Mekkora a kezdőfázisa? Írjuk fel a hullámfüggvényt!VégeredményA hullámfüggvény SI egségekben:
. Mekkora a hullám amplitúdója? Mekkora a kezdőfázisa? Írjuk fel a hullámfüggvényt!VégeredményA hullámfüggvény SI egségekben:![\[y(x,t)=0,0215\sin(80\pi\,t+8,38x+1,95)\]](/images/math/8/b/c/8bccb2c6721257aecd2b946b9944eb7f.png)
- (7.3.) Egy húron csillapítatlan transzverzális hullám terjed
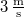 sebességgel pozitív irányban. Amplitúdója
sebességgel pozitív irányban. Amplitúdója 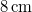 , frekvenciája
, frekvenciája 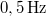 . A
. A  időpillanatban
időpillanatban 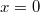 helyen levő részecske kitérése
helyen levő részecske kitérése 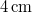 és negatív irányban mozog. Mekkora a kitérése az
és negatív irányban mozog. Mekkora a kitérése az 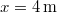 helyen levő részecskének
helyen levő részecskének 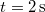 időpillanatban?Végeredmény
időpillanatban?Végeredmény![\[y(4,2)=-8\,\rm{cm}\]](/images/math/e/9/2/e9206020b9dcd879405ea5de4a9635bf.png)
- (7.5.) Egy spirálrugó hosszában longitudinális hullám halad 4 m/s sebességgel. Két egymás után következő sűrűsödési hely távolsága 80 cm, a részecskék rezgési amplitúdója 3 mm. Mekkora a sebességamplitúdó? Mekkora energiával rendelkezik a rezgő rugó egy 0,16 g tömegű részecskéje?Végeredmény
![\[v_{\rm{max}}=9,4\,\rm{\frac{cm}s}\]](/images/math/8/9/b/89ba6ea2494de398fb9909dd294caed6.png)
![\[E=7,1\cdot10^{-7}\,\rm J\]](/images/math/c/b/a/cba6f3a0511d65a1ea80b7291009ac38.png)
- (7.9.) Egy húr hosszirányában két transzverzális hullám fut végig. Mindkettő azonos
 körfrekvenciával és
körfrekvenciával és  amlitúdóval a pozitív
amlitúdóval a pozitív  tengely irányában halad. Az első hullám hatására egy, az origóban levő részecske a
tengely irányában halad. Az első hullám hatására egy, az origóban levő részecske a  időpontban éppen az egyensúlyi helyzeten halad át a pozitív
időpontban éppen az egyensúlyi helyzeten halad át a pozitív  tengely irányában. A második hullám egy negyed hullámhossz útkülönbséggel késik az elsőhöz képest. Adjuk meg a húr tetszés szerinti részecskéjének rezgési egyenletét! Mekkora a kitérés az
tengely irányában. A második hullám egy negyed hullámhossz útkülönbséggel késik az elsőhöz képest. Adjuk meg a húr tetszés szerinti részecskéjének rezgési egyenletét! Mekkora a kitérés az 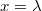 helyen
helyen 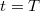 időpontban?ÚtmutatásÁllapítsuk meg a két hullámfüggvényt, és ezekből képezzük az eredő hullám komplex amplitúdóját és hullámfüggvényét!Végeredmény
időpontban?ÚtmutatásÁllapítsuk meg a két hullámfüggvényt, és ezekből képezzük az eredő hullám komplex amplitúdóját és hullámfüggvényét!Végeredmény![\[y(x,t)=\sqrt2A\sin\left(\omega t-kx-\frac{\pi}4\right)\]](/images/math/b/7/3/b7368089cd2251cd9cab6d4ee8168d90.png)
![\[y(\lambda,T)=\sqrt2A\sin\left(-\frac{\pi}4\right)=-A\]](/images/math/f/d/1/fd12f2e467f3e5921a7ca02281c344e5.png)
- (7.15.) Állapítsuk meg egy
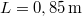 hosszú sípban lévő levegőoszlop
hosszú sípban lévő levegőoszlop 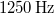 -nél kisebb frekvenciájú rezgéseinek számát! A hang terjedési sebessége
-nél kisebb frekvenciájú rezgéseinek számát! A hang terjedési sebessége 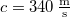 . Legyen a síp
. Legyen a síp
- a) egyik végén zárt,
- b) mindkét végén nyitott!ÚtmutatásÁllapítsuk meg az alaprezgések és felharmonikusok frekvenciáit!VégeredményMindkét esetben 6 db ilyen rezgés van.
- (7.16.) Egy lövedék fejhulláma kúppalástot alkot, amelynek fél nyílásszöge
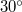 . Mekkora a lövedék sebessége?Végeredmény
. Mekkora a lövedék sebessége?Végeredmény![\[v_f=2c=680\,\rm{\frac ms}\]](/images/math/8/7/a/87ac3b5b0090ee4ca34db7b8c88b0004.png)
- (7.18.) Egy gőzmozdony
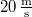 sebességgel közeledik a megfigyelőhöz. Milyen magasnak hallja egy nyugvó megfigyelő a mozdony sípjának alaphangját, ha azt a mozdonyvezető
sebességgel közeledik a megfigyelőhöz. Milyen magasnak hallja egy nyugvó megfigyelő a mozdony sípjának alaphangját, ha azt a mozdonyvezető 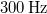 rezgésszámúnak hallja? Mennyivel változik meg e síphang felharmonikusainak frekvenciája? (
rezgésszámúnak hallja? Mennyivel változik meg e síphang felharmonikusainak frekvenciája? (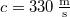 )Végeredmény
)Végeredmény![\[f_1'=319,4\,\rm{Hz}\]](/images/math/8/3/b/83b9e3e93742c07a8aa72013e9638673.png)
![\[\Delta f_n=n\Delta f_1\]](/images/math/0/5/2/0524989863912531160cf5c2b91d0ecb.png)
- (*7.19.) Egy
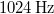 frekvenciájú hangvillát
frekvenciájú hangvillát 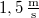 sebességgel közelítünk merőleges irányban egy sima fal felé. Hány lebegést észlel másodpercenként az az álló megfigyelő, aki távolabb a hangvillától annak pályaegyenesén van? Mit hall a hangvillát tartó személy? (
sebességgel közelítünk merőleges irányban egy sima fal felé. Hány lebegést észlel másodpercenként az az álló megfigyelő, aki távolabb a hangvillától annak pályaegyenesén van? Mit hall a hangvillát tartó személy? (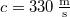 )ÚtmutatásA megfigyelő a hangvilla és a "tükörképe" hangját hallja.Végeredmény
)ÚtmutatásA megfigyelő a hangvilla és a "tükörképe" hangját hallja.Végeredmény![\[f_L=9,309\,\rm{Hz}\]](/images/math/a/2/9/a296d83f132b8c22c86ffdfc433ef778.png)
![\[f_{L2}=9,352\,\rm{Hz}\]](/images/math/4/a/f/4af2b71659fcec43dc465816cf800a21.png)
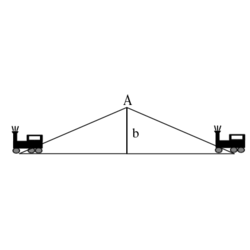
- (*7.21.) Két vonat halad azonos irányban
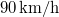 sebességgel, közöttük
sebességgel, közöttük 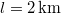 -es közzel. Mit észlel az ábra szerinti
-es közzel. Mit észlel az ábra szerinti  pontban elhelyezkedő megfigyelő, ha a vonatok egyidejűleg
pontban elhelyezkedő megfigyelő, ha a vonatok egyidejűleg 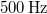 frekvenciájú jelzéseket adnak? (
frekvenciájú jelzéseket adnak? (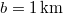 , a hang sebessége
, a hang sebessége 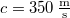 )ÚtmutatásVegyük a sebességek megfelelő irányú komponensét!VégeredményA lebegés frekvenciája
)ÚtmutatásVegyük a sebességek megfelelő irányú komponensét!VégeredményA lebegés frekvenciája![\[f_L=50,6\,\rm{Hz}\]](/images/math/b/5/0/b50edda6007f2d0833abea79dbc29f34.png)
- (*7.22.) Egy kétmotoros repülőgép közvetlenül egy nyugvó megfigyelő felett repül el. A két állandó, de egymástól kissé eltérő fordulatszámmal járó motor lüktető hangot eredményez, amely közeledő gépnél
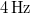 , távolodónál
, távolodónál 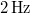 -es lebegésnek bizonyul szélcsendes időben. Mekkora a gép sebessége?ÚtmutatásÍrjuk fel a Doppler eltolódásokat, és vegyük a lebegési frekvenciák hányadosát!Végeredmény
-es lebegésnek bizonyul szélcsendes időben. Mekkora a gép sebessége?ÚtmutatásÍrjuk fel a Doppler eltolódásokat, és vegyük a lebegési frekvenciák hányadosát!Végeredmény![\[v=\frac c3\]](/images/math/c/e/c/cec9006fc404478b873d084e9c34a2fa.png)
- (7.26.) Egy gömbhullámokat kibocsátó, pontszerű hullámforrás az
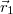 és
és 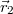 helyzetvektorú pontokat összekötő egyenesen van. Ezekben a pontokban a hullám amplitúdója ismert:
helyzetvektorú pontokat összekötő egyenesen van. Ezekben a pontokban a hullám amplitúdója ismert: 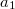 és
és 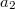 . Adjuk meg a hullámforrás
. Adjuk meg a hullámforrás 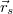 helyzetvektorának kifejezését! (A hullám csillapodása elhanyagolható, a közeg homogén.)Végeredmény
helyzetvektorának kifejezését! (A hullám csillapodása elhanyagolható, a közeg homogén.)Végeredmény![\[x_s=\frac{a_1x_1+a_2x_2}{a_1+a_2}\]](/images/math/2/e/6/2e69b9897d424d6379531acb55e8beec.png)
- (7.28.) Egy
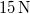 erővel meghúzott húr alaphangja és egy hangvilla hangja
erővel meghúzott húr alaphangja és egy hangvilla hangja 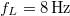 frekvenciájú lebegést eredményez. Ha a húzóerőt
frekvenciájú lebegést eredményez. Ha a húzóerőt 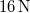 -ra növeljük, akkor a lebegés megszűnik. Mennyi a hangvilla frekvenciája?Végeredmény
-ra növeljük, akkor a lebegés megszűnik. Mennyi a hangvilla frekvenciája?Végeredmény![\[f_h=252\,\rm{Hz}\]](/images/math/1/5/4/1546e3f4e18d5171df0386da198f1bc6.png)
- (7.29.) Számítsuk ki, hogy mekkora energia van egy húr
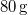 -os részében (feltételezzük, hogy ez a rész sokkal rövidebb a hullámhossznál), ha a húrban
-os részében (feltételezzük, hogy ez a rész sokkal rövidebb a hullámhossznál), ha a húrban 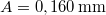 amplitúdójú és
amplitúdójú és 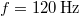 -es hullám terjed!Végeredmény
-es hullám terjed!Végeredmény![\[E=0,58\,\rm{mJ}\]](/images/math/8/3/a/83a33ec09680cb76cf768eda86a71712.png)
- (7.30.) Egy izotróp pontforrás
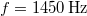 frekvenciájú hullámokat bocsát ki. A forrástól
frekvenciájú hullámokat bocsát ki. A forrástól 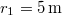 -re a közeg részecskéi
-re a közeg részecskéi 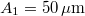 amplitúdójú rezgést végeznek,
amplitúdójú rezgést végeznek, 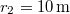 -re pedig az amplitúdó
-re pedig az amplitúdó 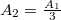 Mennyi a hullám
Mennyi a hullám  csillapítási tényezője? Mennyi a
csillapítási tényezője? Mennyi a 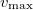 sebességamplitúdó a távolabbi pontban?ÚtmutatásA hullám amplitúdója az 1/r-es faktoron kívül még exponenciálisan is csökken.Végeredmény
sebességamplitúdó a távolabbi pontban?ÚtmutatásA hullám amplitúdója az 1/r-es faktoron kívül még exponenciálisan is csökken.Végeredmény![\[\mu=0,08\,\rm{\frac1m}\]](/images/math/4/0/c/40cc59b0937394c61ff7f602647ace52.png)
![\[v_{\text{max}}=15,2\,\rm{\frac{cm}s}\]](/images/math/d/d/d/ddd3337fb69732483858697e45140dfb.png)
- (**7.8.) Egy
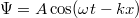 alakú rugalmas síkhullám
alakú rugalmas síkhullám 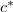 sebességgel terjed a
sebességgel terjed a  közegben. Határozzuk meg ennek a hullámnak a matematikai alakját abban a
közegben. Határozzuk meg ennek a hullámnak a matematikai alakját abban a 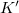 rendszerben, amely az
rendszerben, amely az  tengely irányában a
tengely irányában a  közeghez képest
közeghez képest  sebességgel halad, mind nem-relativisztikus, mind relativisztikus esetben!ÚtmutatásAlkalmazzunk megfelelő koordináta-transzformációt a hullámfüggvény argumentumában, és olvassuk le a mozgó rendszerben észlelhető hullámszámot és körfrekvenciát!
sebességgel halad, mind nem-relativisztikus, mind relativisztikus esetben!ÚtmutatásAlkalmazzunk megfelelő koordináta-transzformációt a hullámfüggvény argumentumában, és olvassuk le a mozgó rendszerben észlelhető hullámszámot és körfrekvenciát!