Mechanika - Két transzverzális hullám
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. december 29., 19:27-kor történt szerkesztése után volt.
Feladat
- (7.9.) Egy húr hosszirányában két transzverzális hullám fut végig. Mindkettő azonos
 körfrekvenciával és
körfrekvenciával és  amlitúdóval a pozitív
amlitúdóval a pozitív  tengely irányában halad. Az első hullám hatására egy, az origóban levő részecske a
tengely irányában halad. Az első hullám hatására egy, az origóban levő részecske a  időpontban éppen az egyensúlyi helyzeten halad át a pozitív
időpontban éppen az egyensúlyi helyzeten halad át a pozitív  tengely irányában. A második hullám egy negyed hullámhossz útkülönbséggel késik az elsőhöz képest. Adjuk meg a húr tetszés szerinti részecskéjének rezgési egyenletét! Mekkora a kitérés az
tengely irányában. A második hullám egy negyed hullámhossz útkülönbséggel késik az elsőhöz képest. Adjuk meg a húr tetszés szerinti részecskéjének rezgési egyenletét! Mekkora a kitérés az 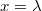 helyen
helyen 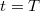 időpontban?
időpontban?
Megoldás
Mindkét rezgéshez rendelhető hullámfügvény, és keressük az eredő hullámüggvényt. Az azonos frekvenciák miatt a hullámhosszak is azonosak (mivel a terjedési sebesség is közös), így a kérdés lényegében az eredő amplitúdó és kezdőfázis. A megadott kezdeti és peremfeltételhez az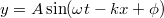 általános alak illeszkedik a legegyszerűbben. Az első hullám esetében így a keződfázis
általános alak illeszkedik a legegyszerűbben. Az első hullám esetében így a keződfázis  , a második esetében a negyedhullámú késés egy
, a második esetében a negyedhullámú késés egy 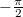 kezdőfázisnak felel meg mindenhol a hullám mentén, tehát az origóban is. Ebben a pontban tekintve két azonos frekvenciájú harmonikus rezgést kell összeadni, például forgóvektoros ábrázolást alkalmazva. Mivel az amplitúdók azonosak és a két vektor merőleges, a vektorháromszögünk derékszögű és egyenlő szárú, így az eredő kezdőfázis
kezdőfázisnak felel meg mindenhol a hullám mentén, tehát az origóban is. Ebben a pontban tekintve két azonos frekvenciájú harmonikus rezgést kell összeadni, például forgóvektoros ábrázolást alkalmazva. Mivel az amplitúdók azonosak és a két vektor merőleges, a vektorháromszögünk derékszögű és egyenlő szárú, így az eredő kezdőfázis 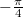 , az eredő amplitúdó pedig
, az eredő amplitúdó pedig 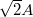 .
. ![\[y(\lambda,T)=y(0,0)=\sqrt2A\sin\left(-\frac{\pi}4\right)=-A\]](/images/math/6/9/4/69477e480987fc3c085110852e1ad871.png)