Mechanika - Állóhullámok sípban

Feladat

1. (7.15.) Állapítsuk meg egy 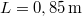$\setbox0\hbox{$L=0,85\,\rm m$}% \message{//depth:\the\dp0//}% \box0%$ hosszú sípban lévő levegőoszlop 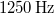$\setbox0\hbox{$1250\,\rm{Hz}$}% \message{//depth:\the\dp0//}% \box0%$-nél kisebb frekvenciájú rezgéseinek számát! A hang terjedési sebessége 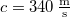$\setbox0\hbox{$c=340\,\rm{\frac ms}$}% \message{//depth:\the\dp0//}% \box0%$. Legyen a síp

   a) egyik végén zárt,

   b) mindkét végén nyitott!

Megoldás

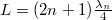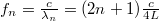Az a) esetben az állóhullámfeltétel $\setbox0\hbox{$L=(2n+1)\frac{\lambda_n}4$}% \message{//depth:\the\dp0//}% \box0%$, így $\setbox0\hbox{$f_n=\frac c{\lambda_n}=(2n+1)\frac c{4L}$}% \message{//depth:\the\dp0//}% \box0%$, ezek rendre 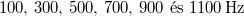$\setbox0\hbox{$100,\, 300,\, 500,\, 700,\, 900\text{ és }1100\,\rm{Hz}$}% \message{//depth:\the\dp0//}% \box0%$ a megadott határon belül, tehát 6 db ilyen rezgés van. 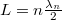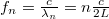A b) esetben az állóhullámfeltétel $\setbox0\hbox{$L=n\frac{\lambda_n}2$}% \message{//depth:\the\dp0//}% \box0%$, így $\setbox0\hbox{$f_n=\frac c{\lambda_n}=n\frac c{2L}$}% \message{//depth:\the\dp0//}% \box0%$, ezek rendre 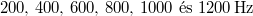$\setbox0\hbox{$200,\,400,\, 600,\,800,\,1000\text{ és }1200\,\rm{Hz}$}% \message{//depth:\the\dp0//}% \box0%$ a megadott határon belül, tehát szintén 6 db ilyen rezgés van.