Mechanika - Gömbhullám
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. december 29., 19:48-kor történt szerkesztése után volt.
Feladat
- (7.26.) Egy gömbhullámokat kibocsátó, pontszerű hullámforrás az
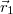 és
és 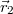 helyzetvektorú pontokat összekötő egyenesen van. Ezekben a pontokban a hullám amplitúdója ismert:
helyzetvektorú pontokat összekötő egyenesen van. Ezekben a pontokban a hullám amplitúdója ismert: 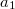 és
és 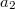 . Adjuk meg a hullámforrás
. Adjuk meg a hullámforrás 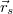 helyzetvektorának kifejezését! (A hullám csillapodása elhanyagolható, a közeg homogén.)
helyzetvektorának kifejezését! (A hullám csillapodása elhanyagolható, a közeg homogén.)
Megoldás
Legyen a pontforrás amplitúdóját jellemző állandó , így tőle tetszőleges
, így tőle tetszőleges 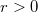 távolságban a tényleges amplitúdó
távolságban a tényleges amplitúdó 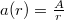 . Legyen az
. Legyen az  tengely az összekötő egyenes, így a problémát egydimneziósan tárgyalhatjuk. Feltéve, hogy a pontforrás az összekötő egyenesen belül az összekötő szakaszon van valahol, azaz
tengely az összekötő egyenes, így a problémát egydimneziósan tárgyalhatjuk. Feltéve, hogy a pontforrás az összekötő egyenesen belül az összekötő szakaszon van valahol, azaz 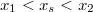 ,
, ![\[a_1=\frac A{x_s-x_1}\]](/images/math/a/0/8/a08373d8348886a5cd540a3064597d32.png)
![\[a_2=\frac A{x_2-x_s}\]](/images/math/c/2/b/c2b8a806cdd29172c665e953f653236d.png)
 -t kiejtve
-t kiejtve ![\[a_1(x_s-x_1)=a_2(x_2-x_s),\]](/images/math/1/e/9/1e9b202d0dbb0984c831283b516f1c43.png)
![\[x_s=\frac{a_1x_1+a_2x_2}{a_1+a_2}\]](/images/math/2/e/6/2e69b9897d424d6379531acb55e8beec.png)