Mechanika - Húr és hangvilla
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. december 29., 18:50-kor történt szerkesztése után volt.
Feladat
- (7.28.) Egy
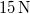 erővel meghúzott húr alaphangja és egy hangvilla hangja
erővel meghúzott húr alaphangja és egy hangvilla hangja 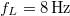 frekvenciájú lebegést eredményez. Ha a húzóerőt
frekvenciájú lebegést eredményez. Ha a húzóerőt 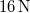 -ra növeljük, akkor a lebegés megszűnik. Mennyi a hangvilla frekvenciája?
-ra növeljük, akkor a lebegés megszűnik. Mennyi a hangvilla frekvenciája?
Megoldás
Legyen a két húzóerő rendre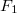 és
és 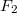 , a két alaphang frekvenciája pedig
, a két alaphang frekvenciája pedig 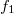 és
és 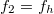 , ahol
, ahol 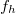 a hangvilla frekvenciája. Mivel a húr hossza adott, a két esetben a hullámhossz is közös, ellenben a terjedési sebesség nem.
a hangvilla frekvenciája. Mivel a húr hossza adott, a két esetben a hullámhossz is közös, ellenben a terjedési sebesség nem. 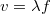 miatt
miatt ![\[\frac{f_1}{f_2}=\frac{v_1}{v_2}=\sqrt{\frac{F_1}{F_2}},\]](/images/math/c/c/b/ccbdf665411496a47133e2a879078955.png)
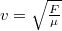 , a húr hosszegységre eső tömege pedig szintén adott. Ezekeből a lebegési frekvencia
, a húr hosszegységre eső tömege pedig szintén adott. Ezekeből a lebegési frekvencia ![\[f_L=f_2-f_1=f_h-f_h\sqrt{\frac{F_1}{F_2}},\]](/images/math/0/b/8/0b8c7b419de0a8ce6b0cba586ffbe4e6.png)
![\[f_h=\frac{f_L}{1-\sqrt{\frac{F_1}{F_2}}}=252\,\rm{Hz}\]](/images/math/6/b/b/6bb25d51c6033e5035d0387ce4223b7f.png)