Mechanika - Csillapodó gömbhullám
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. december 29., 19:54-kor történt szerkesztése után volt.
Feladat
- (7.30.) Egy izotróp pontforrás
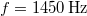 frekvenciájú hullámokat bocsát ki. A forrástól
frekvenciájú hullámokat bocsát ki. A forrástól 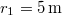 -re a közeg részecskéi
-re a közeg részecskéi 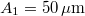 amplitúdójú rezgést végeznek,
amplitúdójú rezgést végeznek, 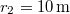 -re pedig az amplitúdó
-re pedig az amplitúdó 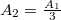 Mennyi a hullám
Mennyi a hullám  csillapítási tényezője? Mennyi a
csillapítási tényezője? Mennyi a 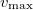 sebességamplitúdó a távolabbi pontban?
sebességamplitúdó a távolabbi pontban?
Megoldás
Csillapodás nélkül kétszeres távolságban fele akkora amplitúdót észlelnénk, de ennek csak a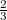 -át észleljük, tehát ez az arány tisztán a csillapodásnak köszönhető. Csillapodó esetben a hullámfüggvény általános alakja
-át észleljük, tehát ez az arány tisztán a csillapodásnak köszönhető. Csillapodó esetben a hullámfüggvény általános alakja ![\[\Psi(r)=\Psi_0\frac{e^{-\mu r}}r\cos(kr),\]](/images/math/4/d/e/4de21e527a79ad31b315ed2db7b933d0.png)
![\[e^{-\mu(r_2-r_1)}=\frac23,\]](/images/math/5/f/e/5fe88026a404a50d2231e5de73e8d0de.png)
![\[\mu=\frac{\ln1,5}{5\,\rm m}=0,08\,\rm{\frac1m}\]](/images/math/9/4/0/9409237e79acb751629f2c560b2a648c.png)
![\[v_{\text{max}}=2\pi f\frac{A_1}3=15,2\,\rm{\frac{cm}s}\]](/images/math/c/0/6/c069aab861c2ed094c460753bfc09e9d.png)