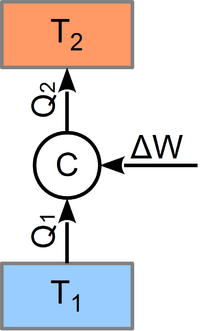
Termodinamika példák - Carnot-hűtőgép
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Stippinger (vitalap | szerkesztései) 2013. április 13., 16:30-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fajhő, Körfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy Carnot-hűtőgép egyik hőtartályában
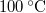 hőmérsékletű, forrásban lévő víz, a másikban
hőmérsékletű, forrásban lévő víz, a másikban 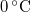 hőmérsékletű víz van. A víz forráshője
hőmérsékletű víz van. A víz forráshője 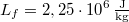 , a jég olvadáshője
, a jég olvadáshője 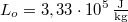 .
.
- a) Mennyi vizet kell az alsó hőtartályban
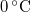 hőmérsékletű jéggé fagyasztani ahhoz, hogy a felső hőtartályban
hőmérsékletű jéggé fagyasztani ahhoz, hogy a felső hőtartályban 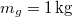 tömegű
tömegű 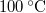 hőmérsékletű gőz keletkezzék?
hőmérsékletű gőz keletkezzék?
- b) Mennyi külső munkát kell a körfolyamatba betáplálni?
- a) Mennyi vizet kell az alsó hőtartályban
Megoldás
Egy körfolyamat hatásfokát a végzett 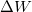 hasznos munkával és a felvett
hasznos munkával és a felvett 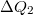 hő nagyságával jellemezzük,
hő nagyságával jellemezzük,
![\[ \eta = \frac{\Delta W}{\Delta Q_2}=\frac{\Delta Q_2-\Delta Q_1}{\Delta Q_2}=1-\frac{\Delta Q_1}{\Delta Q_2}, \]](/images/math/7/b/7/7b71bbe45c5f5bab65847b33fd23d5d4.png)
és Carnot-körfolyamat esetében a hatásfok az adott  alacsony és
alacsony és 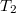 magas hőmérsékletű hőtartályokkal elérhető maximális
magas hőmérsékletű hőtartályokkal elérhető maximális
![\[ \eta_C = 1-\frac{T_1}{T_2}. \]](/images/math/f/9/9/f990941856ba96522db51808a26af213.png)
Most a körfolyamatot hőszivattyáként üzemeltetjük, aminek hatásfoka azonos, de szokás inkább 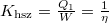 teljesítménytényezővel jellemezni.
teljesítménytényezővel jellemezni.
a) A felírt egyenletekből következik, hogy
![\[ \frac{\Delta Q_1}{\Delta Q_2}=\frac{T_1}{T_2}, \]](/images/math/e/b/6/eb6fcf40a422602230b2422d683484e9.png)
azaz a keletkező jég 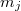 tömegére
tömegére
![\[ \frac{L_o m_j}{L_f m_g}=\frac{T_1}{T_2} \qquad \Rightarrow \qquad m_j= m_g\frac{L_f}{L_o}\frac{T_1}{T_2}. \]](/images/math/a/2/a/a2a6ed7ecdf460ab7816030dba4e38c9.png)
b) Az előzőek alapján a szükséges munka
![\[ \Delta W= \eta \Delta Q_2 = \left(1-\frac{T_1}{T_2}\right) L_f m_g. \]](/images/math/2/3/7/237d48697c77a848be908d378b479ec1.png)