Termodinamika példák - Ideális gáz egy körfolyamata adiabatával

Feladat

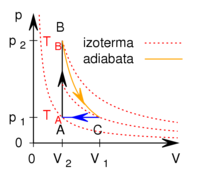
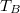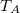1. Az ábrán a $\setbox0\hbox{$T_B$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$T_A$}% \message{//depth:\the\dp0//}% \box0%$ hőmérsékletekkel meghatározott körfolyamat látható. Mekkora annak a gépnek a hatásfoka, amelyik ezt a körfolyamatot mólnyi mennyiségű, adott $\setbox0\hbox{$\gamma$}% \message{//depth:\the\dp0//}% \box0%$ fajhőviszonyú ideális gázzal valósítja meg?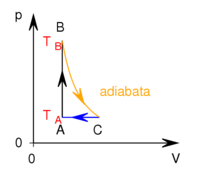
   

Megoldás

A hőerőgép hatásfoka

$\[ \eta = \frac{\Delta W}{\Delta Q_\text{fel}} = \frac{\Delta Q_\text{fel} - |\Delta Q_\text{le}|}{\Delta Q_\text{fel}} = 1-\frac{|\Delta Q_\text{le}|}{\Delta Q_\text{fel}}.\]$

Adiabatától eltérő görbén mozgó rendszer, környezetével hőcserét végez. Jelen körüljárási iránnyal ez az izobár 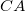$\setbox0\hb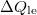ox{$CA$}% \message{//depth:\the\dp0//}% \box0%$ szakaszon $\setbox0\hbox{$\Delta Q_\text{le}$}% \message{//depth:\the\dp0//}% \box0%$ hőleadás, az izochor 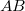$\setbox0\hbox{$AB$}% \message{//depth:\the\dp0//}% \box0%$ szakaszon pedig 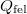$\setbox0\hbox{$Q_\text{fel}$}% \message{//depth:\the\dp0//}% \box0%$ hőfelvétel:

$\[ \Delta Q_\text{le}=n C_p\left( T_C- T_A\right), \]$

$\[ \Delta Q_\text{fel}=n C_V\left( T_B- T_A\right), \]$

behelyettesítve a hatásfok definíciójába:

$\[ \eta= 1-\gamma \frac{T_C-T_A}{T_B-T_A}. \]$

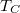$\setbox0\hbox{$T_C$}% \message{//depth:\the\dp0//}% \box0%$-t az adiabata egyenletéből a térfogat és a hőmérséklet segítségével kifejezhetjük:

$\[ T_C V_2^{\gamma-1} = T_B V_1^{\gamma-1} \qquad \Rightarrow \qquad T_C = T_B{\left(\frac{V_1}{V_2}\right)}^{\gamma -1}, \]$

amit az izobár kompresszió 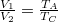$\setbox0\hbox{$\frac{V_1}{V_2}=\frac{T_A}{T_C}$}% \message{//depth:\the\dp0//}% \box0%$ paramétereinek ismeretében visszavezethetünk a megadott hőmérsékletekre:

$\[ T_C^{\gamma }= T_B T_A^{\gamma -1}. \]$

A hatásfok 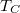$\setbox0\hbox{$T_C$}% \message{//depth:\the\dp0//}% \box0%$ kifejezését behelyettesítve:

$\[ \eta =1-\gamma \frac{T_B^{\frac 1{\gamma }} T_A^{\frac{\gamma -1}{\gamma }}- T_A}{T_B- T_A}=1-\gamma \frac{{\left(\frac{T_B}{T_A}\right)}^{\frac 1{\gamma }}-1}{\frac{T_B}{T_A}-1}.\]$