Termodinamika példák - Ideális gáz egy körfolyamata izotermával
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Fajhő, Körfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
-
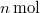 ,
, 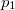 nyomású kétatomos ideális gázt
nyomású kétatomos ideális gázt 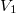 térfogatról állandó nyomáson
térfogatról állandó nyomáson 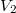 térfogatúra nyomunk össze (az ábrán 1-es út). Ezen az állandó térfogaton eredeti hőmérsékletére melegítjük (2-es út), majd izotermikusan a kiinduló térfogatára tágítjuk (3-as út).
térfogatúra nyomunk össze (az ábrán 1-es út). Ezen az állandó térfogaton eredeti hőmérsékletére melegítjük (2-es út), majd izotermikusan a kiinduló térfogatára tágítjuk (3-as út).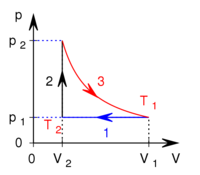
- a) Mennyivel változott a gáz belső energiája az 1-es úton?
- b) Mennyivel hőt kellet közölnünk a gázzal a 2-es úton?
- c) Mekkora a gáz által végzett munka és a gáz által felvett hő a teljes körfolyamatban?
Megoldás
A kétatomos ideális gázt 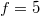 szabadsági fok és
szabadsági fok és 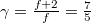 fajhőviszony jellemzi. Az egyes utakat
fajhőviszony jellemzi. Az egyes utakat  ,
,  és
és 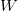 esetében alsó indexben jelöljük.
esetében alsó indexben jelöljük.
a) Az ideális gáz belső energiája kifejezhető a hőmérséklettel, amit pedig az állapotegyenlet segítségével tudunk a megadott adatokra visszavezetni:
![\[ \Delta U_1 = \frac{f}{2}nR\left(T_2-T_1\right) = \frac{f}{2} p_1\left(V_2-V_1\right) = p_1\frac{V_2-V_1}{\gamma-1}. \]](/images/math/e/a/4/ea40d5dd73674a88f012c599218d92f1.png)
b) Izochor átalakulás során nincs térfogati munka, az első főtétel 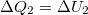 alakot ölti. Mivel a kezdeti hőmérsékletre térünk vissza
alakot ölti. Mivel a kezdeti hőmérsékletre térünk vissza
![\[ \Delta Q_2 = \Delta U_2 = -\Delta U_1. \]](/images/math/6/7/3/6730e1c3dc7b318682c5a6ac8de4fa84.png)
c) Körfolyamat során a rendszer a kiindulási állapotába tér vissza, 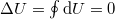 , ezért az első főtétel értelmében
, ezért az első főtétel értelmében
![\[ \oint \delta Q = \oint \delta W = \Delta W_1+\Delta W_2+\Delta W_3 \]](/images/math/9/6/f/96f2a17d8b64d6e75b03ea1c41665474.png)
a három szakaszból számolható, minden felvett hő munkavégzésre fordítódik. Az egyes szakaszok:
-
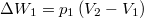 , hiszen az integráljuk értéke a
, hiszen az integráljuk értéke a 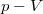 diagrambeli téglalap területe;
diagrambeli téglalap területe;
-
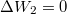 , hiszen nincs térfogatváltozás;
, hiszen nincs térfogatváltozás;
-
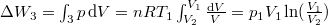 .
.
![\[\Delta Q = \Delta W = p(V_2-V_1)+p_1V_1\ln\left(\frac{V_1}{V_2}\right).\]](/images/math/8/6/0/860eab0c8097201b331e86834ecab3de.png)