| [rejt] Navigáció Pt·1·2·3
|
| Kísérleti fizika gyakorlat 2.
|
Gyakorlatok listája:
- Erőhatások elektromos erőtérben, elektromos térerősség
- Elektromos potenciál
- Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok
- Kapacitás, kondenzátorok. Elrendezések energiája
- Vezetőképesség, áramsűrűség
- Biot-Savart törvény, gerjesztési törvény
- Erőhatások mágneses térben
- Mágneses térerősség. Kölcsönös és öninduktivitás
- Az indukció törvénye, mozgási indukció
- Mágneses tér energiája. Váltakozó áram, eltolási áram
|
| Elektrosztatika - Erőhatások elektromos erőtérben, elektromos térerősség
|
Feladatok listája:
- Négyszög sarkaiba helyezett ponttöltések elektromos tere
- Két töltést összekötő egyenes mentén az elektromos tér
- Körvezető tengelye mentén az elektromos tér
- Egyenletesen töltött körlap tengelye mentén az elektromos tér
- Végtelen hosszú egyenes fonál elektromos tere 1.
- Végtelen hosszú egyenes fonál elektromos tere 2.
- Végtelen sík elektromos tere
- Két, egymásra merőleges végtelen sík elektromos tere
- Homogén térfogati töltéssűrűségű töltött gömb elektromos tere
- Földelt gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
- Egyenletesen töltött gömbben lévő, gömb alakú üreg elektromos tere
- Végtelen hosszú egyenes fonálpár elektromos tere
- Az elektromos térerősség helyfüggő lineáris töltéssűrűségű szigetelő gyűrű tengelye mentén
- Vezető gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064
|
Feladat
- Adott egy
 sugarú korong egyenletesen töltött
sugarú korong egyenletesen töltött  felületi töltéssűrűséggel. Határozzuk meg a térerősséget a körvezető tengelyén, a korong síkjától
felületi töltéssűrűséggel. Határozzuk meg a térerősséget a körvezető tengelyén, a korong síkjától  távolságban!
távolságban!
Megoldás
Induljunk ki az előző feladat megoldásából, amely szerint egy  sugarú,
sugarú,  töltéssel egyenletesen töltött gyűrű tengelyén a térerősség az alábbiak szerint írható le:
töltéssel egyenletesen töltött gyűrű tengelyén a térerősség az alábbiak szerint írható le:
Ahol  a gyűrű síkjától mért távolság.
a gyűrű síkjától mért távolság.
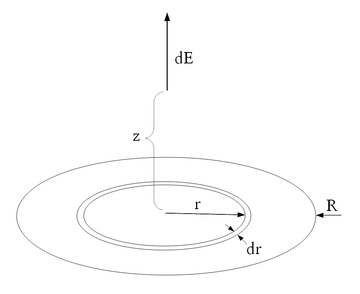
Az  sugarú korongunkat felosztjuk igen vékony,
sugarú korongunkat felosztjuk igen vékony, 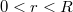 sugarú töltött gyűrűk sokaságára az ábra szerint. Ebben az esetben egy gyűrű
sugarú töltött gyűrűk sokaságára az ábra szerint. Ebben az esetben egy gyűrű 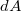 területe:
területe:
Ahol 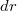 a gyűrű szélessége. Ez alapján a gyűrű
a gyűrű szélessége. Ez alapján a gyűrű 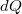 töltése:
töltése:
A gyűrű 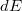 térerősség járuléka a kérdéses pontban:
térerősség járuléka a kérdéses pontban:
Az elemi gyűrűk 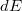 térerősség járulékait összegezzük:
térerősség járulékait összegezzük:
Tehát a korong elektromos tere:
Érdekesség: Ha a korong méretét minden határon túl növeljük, 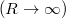 a fenti összefüggés határértéke visszaadja a végtelen síklap jól ismert térerősség formuláját:
a fenti összefüggés határértéke visszaadja a végtelen síklap jól ismert térerősség formuláját:
 sugarú korong egyenletesen töltött
sugarú korong egyenletesen töltött  felületi töltéssűrűséggel. Határozzuk meg a térerősséget a körvezető tengelyén, a korong síkjától
felületi töltéssűrűséggel. Határozzuk meg a térerősséget a körvezető tengelyén, a korong síkjától  távolságban!
távolságban!
 sugarú,
sugarú,  töltéssel egyenletesen töltött gyűrű tengelyén a térerősség az alábbiak szerint írható le:
töltéssel egyenletesen töltött gyűrű tengelyén a térerősség az alábbiak szerint írható le:
![\[ E=\dfrac{Q}{4\pi\varepsilon_{0}}\dfrac{z}{(r^2+z^2)^{3/2}} \]](/images/math/a/c/6/ac6a55602380a259629697b352517c1a.png)
 a gyűrű síkjától mért távolság.
a gyűrű síkjától mért távolság.
 sugarú korongunkat felosztjuk igen vékony,
sugarú korongunkat felosztjuk igen vékony, 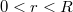 sugarú töltött gyűrűk sokaságára az ábra szerint. Ebben az esetben egy gyűrű
sugarú töltött gyűrűk sokaságára az ábra szerint. Ebben az esetben egy gyűrű 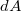 területe:
területe:
![\[ dA=2r\pi dr\]](/images/math/5/e/4/5e42d1d4ea1284b69c3ecae731935466.png)
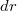 a gyűrű szélessége. Ez alapján a gyűrű
a gyűrű szélessége. Ez alapján a gyűrű 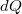 töltése:
töltése:
![\[dQ=\omega dA=2r\pi\omega dr\]](/images/math/6/3/4/63410f2bc422398396f4c935a6a2eae6.png)
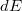 térerősség járuléka a kérdéses pontban:
térerősség járuléka a kérdéses pontban:
![\[ dE=\dfrac{dQ}{4\pi\varepsilon_{0}}\dfrac{z}{(r^2+z^2)^{3/2}}=\dfrac{\omega}{2\varepsilon_{0}}\dfrac{rz}{(r^2+z^2)^{3/2}}dr \]](/images/math/4/2/b/42b7a7d73f08d83ec7e7d336929695fc.png)
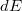 térerősség járulékait összegezzük:
térerősség járulékait összegezzük:
![\[E= \int_0^R dE=\dfrac{z\omega}{2\varepsilon_{0}}\int_0^R\dfrac{r}{(r^2+z^2)^{3/2}}dr=\int_0^R dE=\dfrac{z\omega}{2\varepsilon_{0}} \left[-\dfrac{1}{(r^2+z^2)^{1/2}} \right]_0^R \]](/images/math/4/8/9/489a7377b10fd736be547836aaaf2360.png)
![\[E=\dfrac{\omega}{2\varepsilon_{0}} \left(1-\dfrac{z}{(R^2+z^2)^{1/2}} \right)\]](/images/math/e/7/6/e760b68831c68f2b1ca6a11b95ddee89.png)
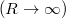 a fenti összefüggés határértéke visszaadja a végtelen síklap jól ismert térerősség formuláját:
a fenti összefüggés határértéke visszaadja a végtelen síklap jól ismert térerősség formuláját:
![\[E=\lim_{R \to \infty}\dfrac{\omega}{2\varepsilon_{0}} \left(1-\dfrac{z}{(R^2+z^2)^{1/2}} \right) = \dfrac{\omega}{2\varepsilon_{0}}\]](/images/math/a/e/a/aeae41530542d272cda166752a72cb3c.png)