| [rejt] Navigáció Pt·1·2·3
|
| Kísérleti fizika gyakorlat 2.
|
Gyakorlatok listája:
- Erőhatások elektromos erőtérben, elektromos térerősség
- Elektromos potenciál
- Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok
- Kapacitás, kondenzátorok. Elrendezések energiája
- Vezetőképesség, áramsűrűség
- Biot-Savart törvény, gerjesztési törvény
- Erőhatások mágneses térben
- Mágneses térerősség. Kölcsönös és öninduktivitás
- Az indukció törvénye, mozgási indukció
- Mágneses tér energiája. Váltakozó áram, eltolási áram
|
| Elektrosztatika - Erőhatások elektromos erőtérben, elektromos térerősség
|
Feladatok listája:
- Négyszög sarkaiba helyezett ponttöltések elektromos tere
- Két töltést összekötő egyenes mentén az elektromos tér
- Körvezető tengelye mentén az elektromos tér
- Egyenletesen töltött körlap tengelye mentén az elektromos tér
- Végtelen hosszú egyenes fonál elektromos tere 1.
- Végtelen hosszú egyenes fonál elektromos tere 2.
- Végtelen sík elektromos tere
- Két, egymásra merőleges végtelen sík elektromos tere
- Homogén térfogati töltéssűrűségű töltött gömb elektromos tere
- Földelt gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
- Egyenletesen töltött gömbben lévő, gömb alakú üreg elektromos tere
- Végtelen hosszú egyenes fonálpár elektromos tere
- Az elektromos térerősség helyfüggő lineáris töltéssűrűségű szigetelő gyűrű tengelye mentén
- Vezető gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064
|
Feladat
- Milyen erőteret hoz létre két, egymásra merőleges végtelen sík, ha rajtuk egyenletesen elosztva
 és
és 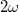 töltéssűrűség van?
töltéssűrűség van?
Megoldás
Az  töltéssűrűségű végtelen síklap körül kialakuló elektromos teret ismerjük a Végtelen sík elektromos tere feladat alapján:
töltéssűrűségű végtelen síklap körül kialakuló elektromos teret ismerjük a Végtelen sík elektromos tere feladat alapján:
Tegyük fel, hogy az  töltéssűrűségű síklap az
töltéssűrűségű síklap az  síkban, míg a
síkban, míg a 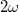 töltéssűrűségű síklap az
töltéssűrűségű síklap az 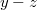 síkban van. Ekkor az
síkban van. Ekkor az  töltéssűrűségű síklap tere az
töltéssűrűségű síklap tere az  tengellyel párhuzamos, helyfüggését az alábbi összefüggés írja le:
tengellyel párhuzamos, helyfüggését az alábbi összefüggés írja le:
Míg a 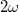 sík tere a következőképp alakul:
sík tere a következőképp alakul:
Az eredő tér ezek szuperpozíciója:
Ahol 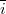 és
és 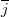 az
az  és
és  irányú egységvektorok.
irányú egységvektorok.
 és
és 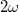 töltéssűrűség van?
töltéssűrűség van?
 töltéssűrűségű végtelen síklap körül kialakuló elektromos teret ismerjük a Végtelen sík elektromos tere feladat alapján:
töltéssűrűségű végtelen síklap körül kialakuló elektromos teret ismerjük a Végtelen sík elektromos tere feladat alapján:
![\[E=\dfrac{\omega}{2\varepsilon_0} \]](/images/math/e/2/6/e26be922b627f50e8d32ed593468c2e1.png)
 töltéssűrűségű síklap az
töltéssűrűségű síklap az  síkban, míg a
síkban, míg a 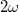 töltéssűrűségű síklap az
töltéssűrűségű síklap az 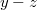 síkban van. Ekkor az
síkban van. Ekkor az  töltéssűrűségű síklap tere az
töltéssűrűségű síklap tere az  tengellyel párhuzamos, helyfüggését az alábbi összefüggés írja le:
tengellyel párhuzamos, helyfüggését az alábbi összefüggés írja le:
![\[E_y=\dfrac{\omega}{2\varepsilon_0}\dfrac{y}{\vert y\vert} \]](/images/math/a/b/d/abd6868ead6fec42481579ce086abd2f.png)
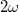 sík tere a következőképp alakul:
sík tere a következőképp alakul:
![\[ E_x=\dfrac{\omega}{\varepsilon_0}\dfrac{x}{\vert x\vert}\]](/images/math/2/2/3/2238ae290e7175d780756b52994ad133.png)
![\[\overline{E}=\dfrac{\omega}{\varepsilon_0}\left( \dfrac{x}{\vert x\vert}\overline{i}+\dfrac{y}{2\vert y\vert}\overline{j} \right)\]](/images/math/8/5/0/85031d55794ce0f5acd93534b092d91f.png)
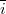 és
és 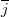 az
az  és
és  irányú egységvektorok.
irányú egységvektorok.