| [rejt] Navigáció Pt·1·2·3
|
| Kísérleti fizika gyakorlat 2.
|
Gyakorlatok listája:
- Erőhatások elektromos erőtérben, elektromos térerősség
- Elektromos potenciál
- Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok
- Kapacitás, kondenzátorok. Elrendezések energiája
- Vezetőképesség, áramsűrűség
- Biot-Savart törvény, gerjesztési törvény
- Erőhatások mágneses térben
- Mágneses térerősség. Kölcsönös és öninduktivitás
- Az indukció törvénye, mozgási indukció
- Mágneses tér energiája. Váltakozó áram, eltolási áram
|
| Elektrosztatika - Erőhatások elektromos erőtérben, elektromos térerősség
|
Feladatok listája:
- Négyszög sarkaiba helyezett ponttöltések elektromos tere
- Két töltést összekötő egyenes mentén az elektromos tér
- Körvezető tengelye mentén az elektromos tér
- Egyenletesen töltött körlap tengelye mentén az elektromos tér
- Végtelen hosszú egyenes fonál elektromos tere 1.
- Végtelen hosszú egyenes fonál elektromos tere 2.
- Végtelen sík elektromos tere
- Két, egymásra merőleges végtelen sík elektromos tere
- Homogén térfogati töltéssűrűségű töltött gömb elektromos tere
- Földelt gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
- Egyenletesen töltött gömbben lévő, gömb alakú üreg elektromos tere
- Végtelen hosszú egyenes fonálpár elektromos tere
- Az elektromos térerősség helyfüggő lineáris töltéssűrűségű szigetelő gyűrű tengelye mentén
- Vezető gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064
|
Feladat
 sugarú szigetelő gömb térfogatában
sugarú szigetelő gömb térfogatában  töltés oszlik el egyenletesen. A gömböt egy véges vastagságú fém gömbhéj veszi körül, melynek görbületi sugarai
töltés oszlik el egyenletesen. A gömböt egy véges vastagságú fém gömbhéj veszi körül, melynek görbületi sugarai  és
és 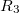 . A gömbhéj eredő töltése 0.
. A gömbhéj eredő töltése 0.
a) Határozzuk meg a szigetelő gömbben a térfogati töltéssűrűséget!
b) Milyen előjelű és milyen nagyságú felületi töltéssűrűség alakul ki az  és
és 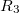 sugarú felületeken?
sugarú felületeken?
c) Határozzuk meg a térerősséget az 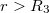 sugáron!
sugáron!
d) Rajzoljuk fel jellegre helyesen az elektromos térerősséget, mint a távolság függvényét!
Megoldás
a)
A gömb térfogati töltéssűrűsége:
b)
A fémfelületen töltésmegosztás jön létre úgy, hogy a fém belsejében a tér nulla lesz, továbbá a fém gömbhéj össztöltése szintén nulla marad. Hogy ez megvalósuljon, a gömbhéj belső,  sugarú felületén
sugarú felületén 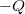 , míg a külső,
, míg a külső, 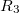 sugarú felületén
sugarú felületén  töltés halmozódik fel. A felületi töltéssűrűségek tehát egyszerűen kiszámíthatóak:
töltés halmozódik fel. A felületi töltéssűrűségek tehát egyszerűen kiszámíthatóak:
illetve:
c)
A fém gömbhéjon kívül a térerősséget nem befolyásolja a gömbhéj. Ez a Gauss-törvénnyel egyszerűen belátható. Tehát a térerősség meghatározható úgy, mintha csak a  töltésű gömb terét kellene kiszámolnunk
töltésű gömb terét kellene kiszámolnunk  távolságban:
távolságban:
d)
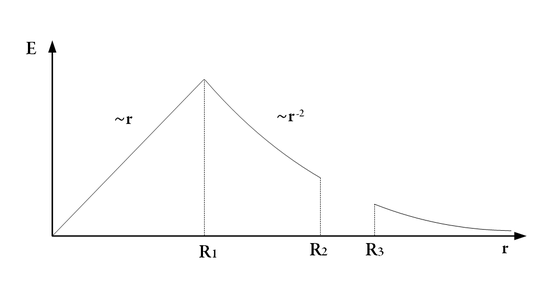
 sugarú szigetelő gömb térfogatában
sugarú szigetelő gömb térfogatában  töltés oszlik el egyenletesen. A gömböt egy véges vastagságú fém gömbhéj veszi körül, melynek görbületi sugarai
töltés oszlik el egyenletesen. A gömböt egy véges vastagságú fém gömbhéj veszi körül, melynek görbületi sugarai  és
és 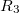 . A gömbhéj eredő töltése 0.
. A gömbhéj eredő töltése 0. és
és 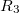 sugarú felületeken?
sugarú felületeken? 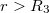 sugáron!
sugáron! ![\[\varrho=\dfrac{Q}{\dfrac{4}{3}R_1^3\pi}\]](/images/math/a/5/a/a5a8d64357cbc4cd512ed3de0c3c745c.png)
 sugarú felületén
sugarú felületén 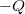 , míg a külső,
, míg a külső, 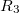 sugarú felületén
sugarú felületén  töltés halmozódik fel. A felületi töltéssűrűségek tehát egyszerűen kiszámíthatóak:
töltés halmozódik fel. A felületi töltéssűrűségek tehát egyszerűen kiszámíthatóak:
![\[\omega_2=\dfrac{-Q}{4R_2^2\pi}\]](/images/math/1/0/b/10b0257aecae9a1ef85eb9a6162234d5.png)
![\[\omega_3=\dfrac{Q}{4R_3^2\pi}\]](/images/math/0/4/b/04b60fad70a1ad31c4d6ebe370f24148.png)
 töltésű gömb terét kellene kiszámolnunk
töltésű gömb terét kellene kiszámolnunk  távolságban:
távolságban:
![\[E=\dfrac{1}{4\pi\varepsilon_0}\dfrac{Q}{r^2}\]](/images/math/c/0/7/c0711a67bf70979b3d447ad9c873f80b.png)
