| [rejt] Navigáció Pt·1·2·3
|
| Kísérleti fizika gyakorlat 2.
|
Gyakorlatok listája:
- Erőhatások elektromos erőtérben, elektromos térerősség
- Elektromos potenciál
- Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok
- Kapacitás, kondenzátorok. Elrendezések energiája
- Vezetőképesség, áramsűrűség
- Biot-Savart törvény, gerjesztési törvény
- Erőhatások mágneses térben
- Mágneses térerősség. Kölcsönös és öninduktivitás
- Az indukció törvénye, mozgási indukció
- Mágneses tér energiája. Váltakozó áram, eltolási áram
|
| Elektrosztatika - Erőhatások elektromos erőtérben, elektromos térerősség
|
Feladatok listája:
- Négyszög sarkaiba helyezett ponttöltések elektromos tere
- Két töltést összekötő egyenes mentén az elektromos tér
- Körvezető tengelye mentén az elektromos tér
- Egyenletesen töltött körlap tengelye mentén az elektromos tér
- Végtelen hosszú egyenes fonál elektromos tere 1.
- Végtelen hosszú egyenes fonál elektromos tere 2.
- Végtelen sík elektromos tere
- Két, egymásra merőleges végtelen sík elektromos tere
- Homogén térfogati töltéssűrűségű töltött gömb elektromos tere
- Földelt gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
- Egyenletesen töltött gömbben lévő, gömb alakú üreg elektromos tere
- Végtelen hosszú egyenes fonálpár elektromos tere
- Az elektromos térerősség helyfüggő lineáris töltéssűrűségű szigetelő gyűrű tengelye mentén
- Vezető gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064
|
Feladat
- Végtelen hosszú egyenes fonálon a lineáris töltéssűrűség
 . Mekkora az elektromos térerősség a fonáltól
. Mekkora az elektromos térerősség a fonáltól  távolságra? ( A keresett térerősséget, pontszerű töltések erőterének szuperpozíciójaként állítsuk elő!)
távolságra? ( A keresett térerősséget, pontszerű töltések erőterének szuperpozíciójaként állítsuk elő!)
Megoldás
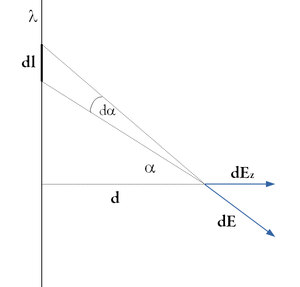
A keresett elektromos teret, pontszerű töltések szuperpozíciójaként állítjuk elő.
A vonaltöltés pontjait a vizsgált pontból a vonaltöltésre állított merőlegeshez mért  látószög szerint parametrizáljuk. A vonaltöltés infinitezimális
látószög szerint parametrizáljuk. A vonaltöltés infinitezimális 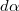 szög alatt látszódó szakasza
szög alatt látszódó szakasza  hosszúságú. Határozzuk meg
hosszúságú. Határozzuk meg  -t
-t  függvényében! A vonaltöltés elemi szakasza és a vizsgált pont közötti
függvényében! A vonaltöltés elemi szakasza és a vizsgált pont közötti  távolság:
távolság:
Ez alapján az ábrán jelölt 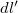 szakasz hossza:
szakasz hossza:
Merőleges szárú szögek tétele alapján belátható, hogy a kérdéses  szakasz hossza:
szakasz hossza:
Ebből a vonaltöltés elemi szakaszának töltése:
Az  szög alatt látszó,
szög alatt látszó, 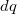 töltésű elemi szakasz terének
töltésű elemi szakasz terének 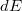 nagysága a kérdéses pontban:
nagysága a kérdéses pontban:
Ezen térerősség vonaltöltésre merőleges 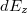 komponense:
komponense:
A fonállal párhuzamos irányú térerősségek kiejtik egymást.
A töltéselrendezés által a kérdéses pontban keltett tér nagyságát integrálással határozhatjuk meg:
Vagyis:
 . Mekkora az elektromos térerősség a fonáltól
. Mekkora az elektromos térerősség a fonáltól  távolságra? ( A keresett térerősséget, pontszerű töltések erőterének szuperpozíciójaként állítsuk elő!)
távolságra? ( A keresett térerősséget, pontszerű töltések erőterének szuperpozíciójaként állítsuk elő!)
 látószög szerint parametrizáljuk. A vonaltöltés infinitezimális
látószög szerint parametrizáljuk. A vonaltöltés infinitezimális 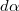 szög alatt látszódó szakasza
szög alatt látszódó szakasza  hosszúságú. Határozzuk meg
hosszúságú. Határozzuk meg  -t
-t  függvényében! A vonaltöltés elemi szakasza és a vizsgált pont közötti
függvényében! A vonaltöltés elemi szakasza és a vizsgált pont közötti  távolság:
távolság:
![\[r=\frac{d}{\cos( \alpha)}\]](/images/math/7/0/0/700b89c56ffa33ac90f60de362460c85.png)
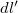 szakasz hossza:
szakasz hossza:
![\[dl'=rd\alpha=\frac{d}{\cos( \alpha)}d\alpha\]](/images/math/4/5/3/453a723fb36d39ec2759d44e52c25707.png)
 szakasz hossza:
szakasz hossza:
![\[dl=\frac{dl'}{\cos( \alpha)}=\frac{d}{\cos{\alpha}^{2}}d\alpha\]](/images/math/4/0/3/403258c46d82690ffb379be51df88bcc.png)
![\[dQ =\lambda dl =\lambda\cdot\frac{d}{\cos{\alpha}^{2}}d\alpha\]](/images/math/9/e/3/9e35e53cf16883fdae8791acb8e83755.png)
 szög alatt látszó,
szög alatt látszó, 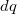 töltésű elemi szakasz terének
töltésű elemi szakasz terének 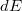 nagysága a kérdéses pontban:
nagysága a kérdéses pontban:
![\[dE = k\cdot\frac{dQ}{r^2}= k\cdot\frac{dQ}{(\frac{d}{\cos{\alpha}})^{2}}\]](/images/math/d/6/f/d6fbbd93dff64d6a38afc4203edd4244.png)
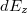 komponense:
komponense:
![\[dE_z =dE\cos(\alpha) = k\cdot\frac{dQ}{(\frac{d}{\cos{\alpha}})^{2}}\cdot\cos{\alpha}\]](/images/math/c/1/3/c1388d4b5198452c694ca2c040c5aad2.png)
![\[E_{z}= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}k\cdot\lambda\cdot\frac{\cos\alpha}{d}d\alpha\]](/images/math/3/6/f/36f13fdc0e631413f953b78a4ead0f51.png)
![\[E_{z} = \frac{2\cdot k\cdot\lambda}{d}\]](/images/math/3/2/5/3252847534a1b7fb7d6b1e0697c9514e.png)