Elektrosztatika példák - Végtelen hosszú egyenes fonál elektromos tere 2.

Feladat

1. Végtelen hosszú egyenes fonálon a lineáris töltéssűrűség $\setbox0\hbox{$\lambda$}% \message{//depth:\the\dp0//}% \box0%$. Határozzuk meg a térerősséget a fonáltól $\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%$ távolságra a Gauss-tétel segítségével!

Megoldás

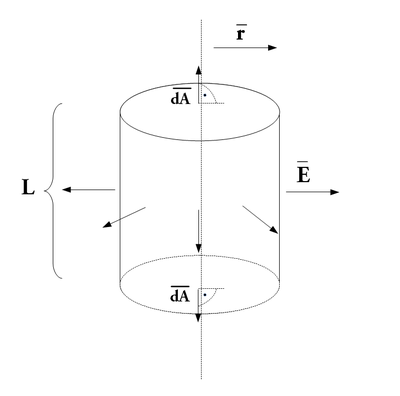
A fonalat vegyük körbe egy $\setbox0\hbox{$L$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú, $\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%$ sugarú hengerrel, és írjuk fel erre a Gauss-tételt:

$\[\iint\vec{E}\cdot\vec{dA} = \frac{1}{\epsilon_{0}}\iiint\rho\cdot dV\]$

A rendszer hengerszimmetriája miatt az elektromos tér mindenütt merőleges a vonaltöltésre, továbbá feltételezhetjük, hogy a vonaltöltéstől adott $\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%$ távolságra elhelyezkedő pontokban a térerősség nagysága állandó. A Gauss törvényben szereplő térerősség henger felületre vett integrálja tehát a következőképp egyszerűsíthető:

-A térerősségnek sehol sincs a henger alapjaira merőleges komponense, így a henger alapjaira vett felületi integrál zérus.

-A henger palástján a térerősség mindenütt merőleges a felületre, abból kifelé mutat, így a felületre vett integrálban szereplő skalárszorzat helyettesíthető a vektorok abszolút értékének szorzatával:

$\[\vec{E}\vec{dA}=EdA\]$

-Mivel a térerősség nagysága a hengerpaláston mindenütt állandó, az integrálást helyettesíthetjük a teljes felület és a konstans térerősség szorzatával:

$\[ \int \int EdA=EA\]$

Ezek alapján az egyszerűsített Gauss törvény:

$\[ E2r\pi L = \frac{\lambda\cdot L}{\epsilon_{0}}\]$

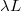Ahol $\setbox0\hbox{$\lambda L$}% \message{//depth:\the\dp0//}% \box0%$ a felület által bezárt töltés. Kifejezve a térerősséget:

$\[E= \frac{\lambda}{2\cdot r\cdot\epsilon_{0}\cdot\pi}\]$

Megjegyzés: Az eredményt érdemes összevetni az előző feladat megoldásával, ahol a Gauss törvény helyett a Coulomb törvényt és a szuperpozíció elvét alkalmazva számoltuk ki a vonaltöltés terét. Láthatjuk, hogy a Gauss törvény alkalmazása jelentősen egyszerűsíti a számolást, ehhez azonban alaposan ki kellett használnunk a rendszer szimmetriáit. Ha a vizsgált töltéselrendezés sérti a fent kihasznált szimmetriákat, a Gauss törvény ilyen formában nem használható. Így például a véges hosszúságú vonaltöltés terének meghatározásakor célravezetőbb az előző példában alkalmazott integrál kiszámítása.