Elektrosztatika példák - Potenciál térerősségből való kiszámolása
A Fizipedia wikiből
Feladat
- Határozzuk meg az
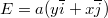 elektromos erőtér potenciálját, ha
elektromos erőtér potenciálját, ha 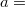 állandó,
állandó, 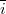 és
és 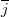 az
az  és
és  tengely irányába mutató egységvektorok!
tengely irányába mutató egységvektorok!
Megoldás
Induljunk ki a potenciál definíciójából:
![\[E=-grad(U)=-\dfrac{\partial U}{\partial x}\overline{i}-\dfrac{\partial U}{\partial y}\overline{j}\]](/images/math/5/c/e/5ce3454cb9a9daea3f6fe64b0e83a300.png)
Ez alapján a következő két egyenletet írhatjuk fel a téresősség ortogonális komponenseire:
![\[E_x=ay=-\dfrac{\partial U}{\partial x}\]](/images/math/5/f/9/5f95bfa5ed5470bf523f0a75d935f8bd.png)
![\[E_y=ax=-\dfrac{\partial U}{\partial y}\]](/images/math/1/4/9/149ede78ff844b4cbbf5d54252c2013b.png)
A fenti összefüggések határozatlan integrálását elvégezve az alábbiakat kapjuk:
![\[U=-\int E_x dx=-axy+C(y)\]](/images/math/f/4/4/f4445b79eb3024dd44699e4dd9609529.png)
![\[U=-\int E_y dy=-axy+C(x)\]](/images/math/f/d/6/fd6e8e75e5d3c476eed3d0f4cc185568.png)
Az integrálok az integrálási változótól független tag erejéig határozatlanok. A fenti két egyenlet csak az alábbi explicit potenciálfüggvénnyel elégíthető ki:
![\[U=-axy+C\]](/images/math/1/7/c/17cbed1f73791320a1d8440c5144e446.png)