Magnetosztatika példák - B és H fluxusa mágneses anyag jelenlétében2

Feladat

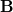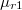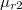1. A mágneses indukció $\setbox0\hbox{$\mathbf{B}$}% \message{//depth:\the\dp0//}% \box0%$ vektorára merőleges sík $\setbox0\hbox{$\mu_{r1}$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$\mu_{r2}$}% \message{//depth:\the\dp0//}% \box0%$ relatív permeabilitású anyagokat választ el egymástól. Tekintsünk egy hengert, melynek $\setbox0\hbox{$S$}% \message{//depth:\the\dp0//}% \box0%$ területű körlapjai párhuzamosak a határfelülettel! 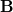Határozzuk meg a $\setbox0\hbox{$\mathbf{B}$}% \message{//depth:\the\dp0//}% \box0%$ mágneses indukció és a 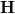$\setbox0\hbox{$\mathbf{H}$}% \message{//depth:\the\dp0//}% \box0%$ mágneses térerősség fluxusát erre a hengerre!

Megoldás

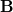A határfelétel szerint $\setbox0\hbox{$\mathbf{B}$}% \message{//depth:\the\dp0//}% \box0%$-nek a normális komponense megy át folytonosan, vagyis

$\[\mathbf{B}_{1N}=\mathbf{B}_{2N}\equiv \mathbf{B}\]$

a mágneses indukció értéke mindkét térrészben.
A fluxust 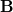$\setbox0\hbox{$\mathbf{B}$}% \message{//depth:\the\dp0//}% \box0%$-nek a hengerre vett felületi integráljaként számolhatjuk:

$\[\Phi_B = \oint \mathbf{B} \mathrm{d}\mathbf{A}\]$

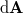Mivel a henger palástján a mágneses indukció merőleges a felületre, ezért az integrálba csak a henger két fedlapja ad járulékot. Mivel a két fedlap területe egyforma ($\setbox0\hbox{$S$}% \message{//depth:\the\dp0//}% \box0%$), de $\setbox0\hbox{$\mathrm{d}\mathbf{A}$}% \message{//depth:\the\dp0//}% \box0%$ iránya ellentétes a két alapkörre, miközben 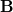$\setbox0\hbox{$\mathbf{B}$}% \message{//depth:\the\dp0//}% \box0%$ iránya és nagysága is megegyezik, a két kör járuléka egymást épp kiejti, így

$\[\Phi_B = 0.\]$

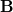A mágneses térerősség a felületre szintén normális, de a határfeltételek szerint különbözik a két térrészben. A $\setbox0\hbox{$\mathbf{B}$}% \message{//depth:\the\dp0//}% \box0%$-re kapott határfeltételből

$\[H_1 = \frac{\mathbf{B}}{\mu_0 \mu_{r1}}\]$

$\[H_2 = \frac{\mathbf{B}}{\mu_0 \mu_{r2}}.\]$

A felületi integrálba megint csak a fedlapok adnak járulékot:

$\[\Phi_H = \oint \mathbf{H}\mathrm{d}\mathbf{A}=-S H_1+S H_2 = \frac{S B}{\mu_0} \left(\frac{1}{\mu_{r2}}-\frac{1}{\mu_{r1}}\right).\]$