Magnetosztatika példák - Két különböző permeabilitású anyagot tartalmazó koaxiális kábel
Feladat
- Egy
 hosszúságú,
hosszúságú, 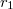 és
és 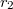 sugarú koaxiális hengerpár közti teret két különböző
sugarú koaxiális hengerpár közti teret két különböző 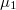 és
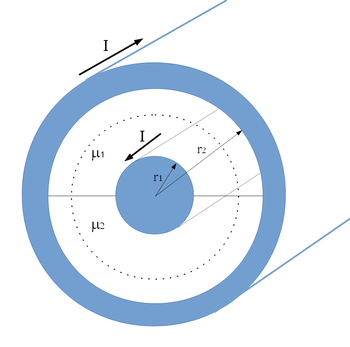
és 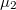 relatív mágneses permeabilitású anyag tölti ki az 1. ábra szerint. A hengerpaláston ellentétes irányban, a tengellyel párhuzamosan folyik
relatív mágneses permeabilitású anyag tölti ki az 1. ábra szerint. A hengerpaláston ellentétes irányban, a tengellyel párhuzamosan folyik  felületi áram. Az áram a belső henger külső felületén folyik, a külső henger vastagságát pedig elhanyagolhatjuk. Mekkora a rendszer öninduktivitása?
felületi áram. Az áram a belső henger külső felületén folyik, a külső henger vastagságát pedig elhanyagolhatjuk. Mekkora a rendszer öninduktivitása?
Megoldás
Áramjárta vezető rendszer  öninduktivitása, és az áramok keltette mágneses tér
öninduktivitása, és az áramok keltette mágneses tér 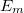 energiája között az alábbi összefüggés írható fel.
energiája között az alábbi összefüggés írható fel.
![\[E_{m}=\dfrac{1}{2}LI^2\]](/images/math/d/3/4/d3413dd5aa07af8f8fde0db6692eff68.png)
Tehát, ha meghatározzuk a tér energiáját, kiszámíthatjuk az öninduktivitást. Ehhez azonban a tér minden pontjában ismernünk kell a mágneses teret.
Az Amper-féle gerjesztési törvényt használva megállapíthatjuk, hogy a hengerpalástokon ellentétes irányokban folyó áramok sem a belső henger belsejében, sem pedig a külső hengerpaláston kívül nem indukálhatnak mágneses teret.
Mágneses tér csak a két koaxiális vezető felület között található. Vegyük fel az ábrán látható zárt görbét, / sugarú kört/ és alkalmazzuk rá az Amper-féle gerjesztési törvényt.
sugarú kört/ és alkalmazzuk rá az Amper-féle gerjesztési törvényt.
![\[ I= \oint \overline{H}d\overline{l}=H_{1}r\pi+H_{2}r\pi\]](/images/math/a/a/d/aad3fd11ed97f336ea858d3563bb0fe9.png)
Ahol 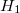 és
és 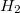 a két közegben mérhető mágneses gerjesztés értéke. Kihasználva azt, hogy a mágneses indukció közeghatárra merőleges komponense folytonosan megy át a közeghatáron, a gerjesztési törvény az alábbiak szerint alakítható.
a két közegben mérhető mágneses gerjesztés értéke. Kihasználva azt, hogy a mágneses indukció közeghatárra merőleges komponense folytonosan megy át a közeghatáron, a gerjesztési törvény az alábbiak szerint alakítható.
![\[I=\dfrac{B}{\mu_{0}\mu_{1}}r\pi+\dfrac{B}{\mu_{0}\mu_{2}}r\pi\]](/images/math/8/4/2/8427f459166a5310e4ecceba474380bd.png)
Ebből kifejezhető a mágneses indukció:
![\[ B=\dfrac{\mu_{0}I}{r\pi}\dfrac{\mu_{1}\mu_{2}}{\mu_{1}+\mu_{2}} \]](/images/math/3/4/4/344580cf3cb50db8f33fe5f82256fa9e.png)
A mágnes indukció ismeretében explicit módon kifejezhetőek a két közegben fellépő mágneses gerjesztés értékei a középvonaltól mért  távolság függvényében:
távolság függvényében:
![\[ H_{1}=\dfrac{I}{r\pi}\dfrac{\mu_{2}}{\mu_{1}+\mu_{2}} \]](/images/math/1/3/a/13a92e54c41d1d947680b4e7992bf517.png)
![\[ H_{2}=\dfrac{I}{r\pi}\dfrac{\mu_{1}}{\mu_{1}+\mu_{2}} \]](/images/math/5/e/a/5eade6b8b58c883ee0fe52188384fa92.png)
A fentiek ismeretében meghatározható a két térrész mágneses energia sűrűsége a  függvényében.
függvényében.
![\[e_{1}=\dfrac{1}{2}H_{1}B=\dfrac{I^2\mu_{0}\mu_{1}\mu_{2}^2}{2\pi^2(\mu_{1}+\mu_{2})^2}\dfrac{1}{r^2}\]](/images/math/e/3/c/e3cf8963cad1bb619c43a36c4dcd0798.png)
![\[e_{2}=\dfrac{1}{2}H_{2}B=\dfrac{I^2\mu_{0}\mu_{1}^2\mu_{2}}{2\pi^2(\mu_{1}+\mu_{2})^2}\dfrac{1}{r^2}\]](/images/math/e/f/c/efcaf4bfca8f9561ccd2cd1e278a4d71.png)
Az energiasűrűséget a két hengerfelület közti térfogatra integrálva meghatározhatjuk a mágneses tér energiáját.
![\[ E_m=l\int\limits_{r_{1}}^{r_{2}} \int\limits_{0}^{\pi} e_{1}rd\varphi dr + l\int\limits_{r_{1}}^{r_{2}} \int\limits_{\pi}^{2\pi} e_{2}rd\varphi dr = l\pi \int\limits_{r_{1}}^{r_{2}} (e_{1}+e_{1})r dr\]](/images/math/7/1/c/71c0fd7056d8420955c809ef3e58ca31.png)
Behelyettesítve az 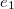 és
és 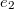 energia sűrűségeket az egyszerűsítés után az alábbi integrált kapjuk:
energia sűrűségeket az egyszerűsítés után az alábbi integrált kapjuk:
![\[E_m=\dfrac{l\mu_0 I^2 \mu_1 \mu_2}{2\pi(\mu_1+\mu_2)} \int\limits_{r_{1}}^{r_{2}} \dfrac{1}{r} dr \]](/images/math/d/1/0/d103c782b82c13c882a5fc6523ed22f2.png)
A mágneses tér energiája tehát:
![\[E_m=\dfrac{l\mu_0 I^2 \mu_1 \mu_2}{2\pi(\mu_1+\mu_2)} ln \dfrac{r_{2}}{r_{1}}\]](/images/math/2/c/c/2cce23a21a2869506e839892adec5b9c.png)
Az elrendezés önindukciós együtthatója a tér energiájából az alábbi egyenlet segítségével határozható meg.
![\[E_{m}= \dfrac{l\mu_0 I^2 \mu_1 \mu_2}{2\pi(\mu_1+\mu_2)} ln \dfrac{r_{2}}{r_{1}} =\dfrac{1}{2}LI^2\]](/images/math/a/1/2/a127ba22117284a6dd4d11e8aafbbea6.png)
Az önindukciós együttható:
![\[L= \dfrac{l\mu_0 \mu_1 \mu_2}{\pi(\mu_1+\mu_2)} ln \dfrac{r_{2}}{r_{1}}\]](/images/math/b/7/2/b720ba8b9d03318424802472b3da728c.png)