„Mechanika - Rugókra merőleges rezgés” változatai közötti eltérés
(→Megoldás) |
|||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 13. sor: | 13. sor: | ||
$x=0$ egyensúlyi helyzet esetén a rugó megnyúlása $l-l_0$. Kimozdítva onnan a rugó hossza $l$ helyett már $l_2$, és $$x^2+l^2=l_2^2$$. A rugóerő $F_r=-D(l_2-l_0)$, de ez rugóirányú, ennek csak az $x$ irányú vetülete jelenik meg az $x$ irányú mozgásegyenletben. A sín és a rugó által bezárt szöget $\alpha$-val jelölve $$F_x=F_r\cos{\alpha}=F_r\frac xl_2$$ $l_2$ a fenti Pitagorasz-tételből kifejezhető, azonban a mozgásegyenlet így még túl általános, nem harmonikus rezgést ír le, ehhez ugyanis alkalmazni kell a kis kitérés közelítését is. | $x=0$ egyensúlyi helyzet esetén a rugó megnyúlása $l-l_0$. Kimozdítva onnan a rugó hossza $l$ helyett már $l_2$, és $$x^2+l^2=l_2^2$$. A rugóerő $F_r=-D(l_2-l_0)$, de ez rugóirányú, ennek csak az $x$ irányú vetülete jelenik meg az $x$ irányú mozgásegyenletben. A sín és a rugó által bezárt szöget $\alpha$-val jelölve $$F_x=F_r\cos{\alpha}=F_r\frac xl_2$$ $l_2$ a fenti Pitagorasz-tételből kifejezhető, azonban a mozgásegyenlet így még túl általános, nem harmonikus rezgést ír le, ehhez ugyanis alkalmazni kell a kis kitérés közelítését is. | ||
Erre számos módszer kínálkozik. Az egyik az $l_2(x)$ függvény sorbafejtése, ez $$l_2(x)=\sqrt{x^2+l^2}=l\sqrt{1+\frac{x^2}{l^2}}\approx l\left(1+\frac{x^2}{2l^2}\right)$$ Ennek második tagja $F_x$ kifejezésébe beírva összességében $x$-ben harmadrendű, tehát elhagyható, ami azt is jelenti, hogy $l_2$ elsőrendű közelítésben egyenlő $l$-el, mivel a sorfejtésben nincs $x$-el arányos lineáris tag, csak másodrendű $x^2$-tel arányos. Így a visszatérítő erő végül: $$F_x\approx -D(l-l_0)\frac xl,$$ vagyis az effektív rugóállandó $$D_{\rm{eff}}=D\frac{l-l_0}l$$ | Erre számos módszer kínálkozik. Az egyik az $l_2(x)$ függvény sorbafejtése, ez $$l_2(x)=\sqrt{x^2+l^2}=l\sqrt{1+\frac{x^2}{l^2}}\approx l\left(1+\frac{x^2}{2l^2}\right)$$ Ennek második tagja $F_x$ kifejezésébe beírva összességében $x$-ben harmadrendű, tehát elhagyható, ami azt is jelenti, hogy $l_2$ elsőrendű közelítésben egyenlő $l$-el, mivel a sorfejtésben nincs $x$-el arányos lineáris tag, csak másodrendű $x^2$-tel arányos. Így a visszatérítő erő végül: $$F_x\approx -D(l-l_0)\frac xl,$$ vagyis az effektív rugóállandó $$D_{\rm{eff}}=D\frac{l-l_0}l$$ | ||
| − | A másik lehetőség a Pitagorasz-tétel négyzetes alakjának teljes differenciálját képezni, mindkét oldalon a saját $x$ és $l_2$ változó szerint. (Emlékezzünk, hogy $l$ minimális, de előfeszített hossz adott állandó paraméter!) Ebből: $2x\rm dx=2l_2\rm dl_2$ kapható, azaz a rugó kis hosszváltozása $$\rm dl_2=\frac{x}{l_2}\rm dx=\cos{\alpha}\rm dx$$ Ez utóbbi alakot egy megfelelő rajzból is felírhattuk volna, amely a sínen történő kis $\rm dx$ elmozdulást a rugó kis $\rm dl_2$ megnyúlásával veti össze, ez lett volna a harmadik, grafikus módszer.[[Kép:Kfgy1-6-9M.svg|none|250px]] | + | A másik lehetőség a Pitagorasz-tétel négyzetes alakjának teljes differenciálját képezni, mindkét oldalon a saját $x$ és $l_2$ változó szerint. (Emlékezzünk, hogy $l$ minimális, de előfeszített hossz adott állandó paraméter!) Ebből: $2x\rm dx=2l_2\rm dl_2$ kapható, azaz a rugó kis hosszváltozása $$\rm dl_2=\frac{x}{l_2}\rm dx=\cos{\alpha}\rm dx$$ Ez utóbbi alakot egy megfelelő rajzból is felírhattuk volna, amely a sínen történő kis $\rm dx$ elmozdulást a rugó kis $\rm dl_2$ megnyúlásával veti össze, ez lett volna a harmadik, grafikus módszer.[[Kép:Kfgy1-6-9M.svg|none|250px]] A rugóerő ezt a közelítést felhasználva $$F_r=-D(l_2-l_0)=-D(l+\rm dl_2-l_0)=-D(l-l_0+\cos{\alpha}\rm dx)$$ önmagában még látszólag lineáris $dx$-ben, de $\cos{\alpha}$ szintén kicsi ($<<1$) és a kis kitéréssel arányos, tehát ez a tag másodrendű, így elhagyható. H azonban ezt ebből még nem látnánk, képezzük $F_x$-et: $$F_x=-D(l-l_0)\cos{\alpha}-D\cos^2{\alpha}\rm dx$$ Mivel kis kitérésekre $\alpha\approx 90^{\circ}$, így $\cos{\alpha}\ll 1$ és $\cos^2{\alpha}\ll \cos{\alpha}$, tehát a második tag még akkor is elhagyható, ha $\rm dx$ összemérhető $l-l_0$ előfeszítéssel. |
Összességében tehát azt látjuk, hogy előfeszítés nélkül nem lesz harmonikus rezgés, mivel annak frekvenciájára nulla adódna. (Lásd feszítetlen gitárhúr) Másodsorban a relatív előfeszítés számít, és annak négyzetgyökével arányos a frekvencia. Harmadrészt $l\gg l_0$ esetén (azaz $l\rightarrow\infty$ határesetben) visszakapjuk a rugó $D$ állandóját.</wlatex> | Összességében tehát azt látjuk, hogy előfeszítés nélkül nem lesz harmonikus rezgés, mivel annak frekvenciájára nulla adódna. (Lásd feszítetlen gitárhúr) Másodsorban a relatív előfeszítés számít, és annak négyzetgyökével arányos a frekvencia. Harmadrészt $l\gg l_0$ esetén (azaz $l\rightarrow\infty$ határesetben) visszakapjuk a rugó $D$ állandóját.</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. augusztus 29., 13:47-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rezgések I. |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
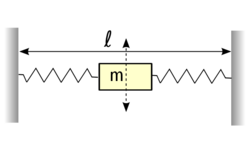
- (*6.9.) Két vízszintes helyzetű
 rugóállandójú rugó közé
rugóállandójú rugó közé  tömegű anyagi pontot erősítünk, amely vertikálisan kis amplitúdóval rezgéseket végez. A két rugó összhossza nyugalmi állapotban
tömegű anyagi pontot erősítünk, amely vertikálisan kis amplitúdóval rezgéseket végez. A két rugó összhossza nyugalmi állapotban 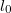 , megfeszítve
, megfeszítve  . Határozzuk meg a rezgési frekvenciát, mint
. Határozzuk meg a rezgési frekvenciát, mint  függvényét, ha kis amplitúdójú rezgéseket engedünk csak meg. Vizsgáljuk az
függvényét, ha kis amplitúdójú rezgéseket engedünk csak meg. Vizsgáljuk az 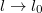 határesetet!
határesetet!
Megoldás
A rezgési frekvencia meghatározásához fel kell írni a rugókra merőleges irányú mozgásegyenletet, azaz a visszatérítő erőt az ez irányú kitérés függvényében. Mivel a két rugó azonos hatású, kezelhetjük a feladatot úgy is, hogy csak egy rugót tekintünk, és a testet úgy képzeljük, mintha egy függőleges súrlódásmentes sínen tudna csúszkálni. Az erre az esetre meghatározott effektív rugóállandó kétszerese lesz a valóságos a két rugó esetén.
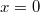 egyensúlyi helyzet esetén a rugó megnyúlása
egyensúlyi helyzet esetén a rugó megnyúlása 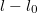 . Kimozdítva onnan a rugó hossza
. Kimozdítva onnan a rugó hossza  helyett már
helyett már 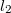 , és
, és ![\[x^2+l^2=l_2^2\]](/images/math/e/5/3/e53c4b6041f9973d792dcfe2b1e96598.png)
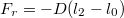 , de ez rugóirányú, ennek csak az
, de ez rugóirányú, ennek csak az  irányú vetülete jelenik meg az
irányú vetülete jelenik meg az  irányú mozgásegyenletben. A sín és a rugó által bezárt szöget
irányú mozgásegyenletben. A sín és a rugó által bezárt szöget  -val jelölve
-val jelölve ![\[F_x=F_r\cos{\alpha}=F_r\frac xl_2\]](/images/math/5/c/0/5c0a79532f16e90060ea3c2a18628f7e.png)
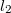 a fenti Pitagorasz-tételből kifejezhető, azonban a mozgásegyenlet így még túl általános, nem harmonikus rezgést ír le, ehhez ugyanis alkalmazni kell a kis kitérés közelítését is.
Erre számos módszer kínálkozik. Az egyik az
a fenti Pitagorasz-tételből kifejezhető, azonban a mozgásegyenlet így még túl általános, nem harmonikus rezgést ír le, ehhez ugyanis alkalmazni kell a kis kitérés közelítését is.
Erre számos módszer kínálkozik. Az egyik az 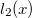 függvény sorbafejtése, ez
függvény sorbafejtése, ez ![\[l_2(x)=\sqrt{x^2+l^2}=l\sqrt{1+\frac{x^2}{l^2}}\approx l\left(1+\frac{x^2}{2l^2}\right)\]](/images/math/b/1/a/b1a5b521c02a5bc904ba3d0e60992dd5.png)
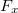 kifejezésébe beírva összességében
kifejezésébe beírva összességében  -ben harmadrendű, tehát elhagyható, ami azt is jelenti, hogy
-ben harmadrendű, tehát elhagyható, ami azt is jelenti, hogy 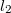 elsőrendű közelítésben egyenlő
elsőrendű közelítésben egyenlő  -el, mivel a sorfejtésben nincs
-el, mivel a sorfejtésben nincs  -el arányos lineáris tag, csak másodrendű
-el arányos lineáris tag, csak másodrendű 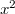 -tel arányos. Így a visszatérítő erő végül:
-tel arányos. Így a visszatérítő erő végül: ![\[F_x\approx -D(l-l_0)\frac xl,\]](/images/math/b/b/b/bbb98790a83d7996bb53c048209fc493.png)
![\[D_{\rm{eff}}=D\frac{l-l_0}l\]](/images/math/3/f/e/3fe4e29b79562fe1c65dded8196a4d26.png)
 és
és 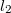 változó szerint. (Emlékezzünk, hogy
változó szerint. (Emlékezzünk, hogy  minimális, de előfeszített hossz adott állandó paraméter!) Ebből:
minimális, de előfeszített hossz adott állandó paraméter!) Ebből: 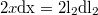 kapható, azaz a rugó kis hosszváltozása
kapható, azaz a rugó kis hosszváltozása ![\[\rm dl_2=\frac{x}{l_2}\rm dx=\cos{\alpha}\rm dx\]](/images/math/a/b/8/ab8196f0ac387354865de60523d77685.png)
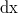 elmozdulást a rugó kis
elmozdulást a rugó kis 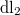 megnyúlásával veti össze, ez lett volna a harmadik, grafikus módszer. A rugóerő ezt a közelítést felhasználva
megnyúlásával veti össze, ez lett volna a harmadik, grafikus módszer. A rugóerő ezt a közelítést felhasználva ![\[F_r=-D(l_2-l_0)=-D(l+\rm dl_2-l_0)=-D(l-l_0+\cos{\alpha}\rm dx)\]](/images/math/f/b/1/fb10d1c743e47486d9d1d55c823c0c67.png)
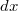 -ben, de
-ben, de 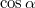 szintén kicsi (
szintén kicsi (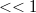 ) és a kis kitéréssel arányos, tehát ez a tag másodrendű, így elhagyható. H azonban ezt ebből még nem látnánk, képezzük
) és a kis kitéréssel arányos, tehát ez a tag másodrendű, így elhagyható. H azonban ezt ebből még nem látnánk, képezzük 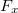 -et:
-et: ![\[F_x=-D(l-l_0)\cos{\alpha}-D\cos^2{\alpha}\rm dx\]](/images/math/f/3/d/f3d8dc5afd65d212b3dc3943265e61d7.png)
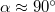 , így
, így 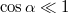 és
és 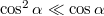 , tehát a második tag még akkor is elhagyható, ha
, tehát a második tag még akkor is elhagyható, ha 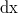 összemérhető
összemérhető 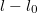 előfeszítéssel.
előfeszítéssel.
Összességében tehát azt látjuk, hogy előfeszítés nélkül nem lesz harmonikus rezgés, mivel annak frekvenciájára nulla adódna. (Lásd feszítetlen gitárhúr) Másodsorban a relatív előfeszítés számít, és annak négyzetgyökével arányos a frekvencia. Harmadrészt 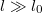 esetén (azaz
esetén (azaz 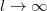 határesetben) visszakapjuk a rugó
határesetben) visszakapjuk a rugó  állandóját.
állandóját.