„Mechanika - Inga kétféle rezgésideje” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
(→Feladat) |
||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (*6.11.) Mutassuk meg, hogy egy | + | </noinclude><wlatex># (*6.11.) Mutassuk meg, hogy egy kúpinga periódusideje ugyanakkora, ha egy kis kör mentén mozog, mint ha síkban kis lengéseket végez!</wlatex><includeonly><wlatex>{{Végeredmény|content=A körfrekvencia négyzete mindkét esetben $$\omega^2=\frac gl$$}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>Elegendő megmutatni a körfrekvenciák (négyzetének) azonosságát. Sík lengések esetén a tangenciális mozgásegyenlet $$ma_t=m\ddot{\alpha}l=-mg\sin{\alpha}\approx-mg\alpha,$$ ahol $l$ az inga hossza. Ebből a szöggyorulásra rendezve lelolvasható a körfrekvencia (négyzete) $$\omega^2=\frac gl$$ A körözés esetén a körmozgás vízszintes síkban zajlik és egyenletes, ezért a mozgásegyenletet vízszintes radiális, és függőleges komponenesekre írjuk fel. (Ebben az esetben nincsenek tangenciális erők és gyorsulás.) $$K\cos{\alpha}=mg$$ $$K\sin{\alpha}=m\omega^2r,$$ ahol $K$ a kötélerő, és $r$ a körpálya sugara. Mivel $r\ll l$, így $\sin{\alpha}=\frac rl\approx\tan{\alpha}$, másrészt a két fenti egyenletet egymással elosztva $$\tan{\alpha}=\frac{\omega^2r}g,$$ így $\frac{\omega^2}g=\frac1l$, ebből pedig $$\omega^2=\frac gl,$$ ami egyezik az előző esetben kapott eredménnyel.</wlatex> | + | <wlatex>Elegendő megmutatni a körfrekvenciák (négyzetének) azonosságát. Sík lengések esetén a tangenciális mozgásegyenlet $$ma_t=m\ddot{\alpha}l=-mg\sin{\alpha}\approx-mg\alpha,$$ ahol $l$ az inga hossza. Ebből a szöggyorulásra rendezve lelolvasható a körfrekvencia (négyzete) $$\omega^2=\frac gl$$ A körözés esetén a körmozgás vízszintes síkban zajlik és egyenletes, ezért a mozgásegyenletet vízszintes radiális, és függőleges komponenesekre írjuk fel. (Ebben az esetben nincsenek tangenciális erők és gyorsulás.) $$K\cos{\alpha}=mg$$ $$K\sin{\alpha}=m\omega^2r,$$ ahol $K$ a kötélerő, és $r$ a körpálya sugara. Mivel $r\ll l$, így $\sin{\alpha}=\frac rl\approx\tan{\alpha}$, másrészt a két fenti egyenletet egymással elosztva $$\tan{\alpha}=\frac{\omega^2r}g,$$ így $\frac{\omega^2}g=\frac1l$, ebből pedig $$\omega^2=\frac gl,$$ ami egyezik az előző esetben kapott eredménnyel.[[Kép:Kfgy1_6_11m.svg|none|250px]]</wlatex> |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. augusztus 29., 13:48-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rezgések I. |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
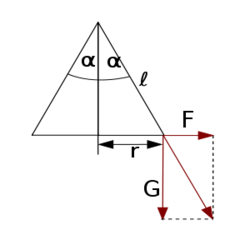
Feladat
- (*6.11.) Mutassuk meg, hogy egy kúpinga periódusideje ugyanakkora, ha egy kis kör mentén mozog, mint ha síkban kis lengéseket végez!
Megoldás
Elegendő megmutatni a körfrekvenciák (négyzetének) azonosságát. Sík lengések esetén a tangenciális mozgásegyenlet![\[ma_t=m\ddot{\alpha}l=-mg\sin{\alpha}\approx-mg\alpha,\]](/images/math/8/b/4/8b447e9d0f5bfdb93c44981334cef6c0.png)
 az inga hossza. Ebből a szöggyorulásra rendezve lelolvasható a körfrekvencia (négyzete)
az inga hossza. Ebből a szöggyorulásra rendezve lelolvasható a körfrekvencia (négyzete) ![\[\omega^2=\frac gl\]](/images/math/e/8/6/e869d041559ef36b3aab46f5685284e8.png)
![\[K\cos{\alpha}=mg\]](/images/math/1/8/8/1885409cd4829296676256e5a4cec46d.png)
![\[K\sin{\alpha}=m\omega^2r,\]](/images/math/4/0/c/40c6e5c6d97169b593ae4a2e06a73e92.png)
 a kötélerő, és
a kötélerő, és  a körpálya sugara. Mivel
a körpálya sugara. Mivel 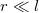 , így
, így 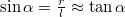 , másrészt a két fenti egyenletet egymással elosztva
, másrészt a két fenti egyenletet egymással elosztva ![\[\tan{\alpha}=\frac{\omega^2r}g,\]](/images/math/f/7/6/f7646585ec7d91a10ab4d573df1d0153.png)
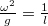 , ebből pedig
, ebből pedig ![\[\omega^2=\frac gl,\]](/images/math/d/1/9/d19058f31374cb77aff2bf021770173b.png)