„Elektrosztatika példák - Végtelen sík elektromos tere” változatai közötti eltérés
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 2. Kategória:Szerkesztő:Beleznai Kategória:Elektrosztatika {{Kísérleti fizika gyakorlat | tárgynév …”) |
(→Megoldás) |
||
| (egy szerkesztő 8 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex>#Végtelen kiterjedésű síkon $\omega$ felületi töltéssűrűség van. Határozzuk meg a térerősséget a Gauss-tétel segítségével a síktól $z$ távolságra!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$E=\dfrac{\omega}{2\varepsilon_0} $$ | + | </noinclude><wlatex>#Végtelen kiterjedésű síkon $\omega$ felületi töltéssűrűség van. Határozzuk meg a térerősséget a Gauss-tétel segítségével a síktól $z$ távolságra!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$E=\dfrac{\omega}{2\varepsilon_0} $$}} |
</wlatex></includeonly><noinclude> | </wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
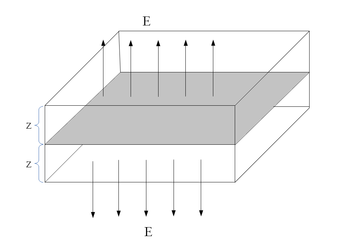
| − | A Gauss-tétel alkalmazásához fel kell vennünk egy zárt felületet a térben. Ez legyen egy téglatest, melynek a töltött síkkal párhuzamos lapjai egyenként $A$ területűek. Az $A$ területű lapok a töltött sík átellenes oldalain helyezkednek el, attól egyaránt $z$ távolságra. ( | + | [[Kép:KFGY2-1-7.png|none|350px]] |
| + | A Gauss-tétel alkalmazásához fel kell vennünk egy zárt felületet a térben. Ez legyen egy téglatest, melynek a töltött síkkal párhuzamos lapjai egyenként $A$ területűek. Az $A$ területű lapok a töltött sík átellenes oldalain helyezkednek el, attól egyaránt $z$ távolságra. (ábra) Az így definiált téglateste írjuk fel a Gauss-törvényt: | ||
$$\dfrac{Q}{\varepsilon_0}=\oint \overline{E} \overline{dA}$$ | $$\dfrac{Q}{\varepsilon_0}=\oint \overline{E} \overline{dA}$$ | ||
Ahol $Q=A\omega$ a felvett téglatest által bezárt töltés mennyisége. | Ahol $Q=A\omega$ a felvett téglatest által bezárt töltés mennyisége. | ||
| − | A rendszer szimmetriája miatt kijelenthetjük, hogy az elektromos tér mindenütt merőleges lesz a töltött síkra. Ebből következik, hogy a téglatest töltött síkra merőleges oldalfalain az $\overline{E} \overline{dA}$ skalárszorzat minden pontban azonosan nulla lesz, hiszen ezen felületek normálisa mindenütt $90^o$-os szöget zár be a | + | A rendszer szimmetriája miatt kijelenthetjük, hogy az elektromos tér mindenütt merőleges lesz a töltött síkra. Ebből következik, hogy a téglatest töltött síkra merőleges oldalfalain az $\overline{E} \overline{dA}$ skalárszorzat minden pontban azonosan nulla lesz, hiszen ezen felületek normálisa mindenütt $90^o$-os szöget zár be a $\overline{E}$ térerősséggel. |
| − | A töltött síkkal párhuzamos $A$ felületű lapokon viszont a $\overline{dA}$ felületnormális és a | + | A töltött síkkal párhuzamos $A$ felületű lapokon viszont a $\overline{dA}$ felületnormális és a $\overline{E}$ térerősség minden pontban párhuzamos egymással, így azok skalárszorzata megegyezik a vektorok abszolút értékének szorzatával: $\overline{E} \overline{dA}=EdA$ |
| + | |||
| + | A térerősség zárt felületre felvett integrálja az alábbi formára egyszerűsödik: | ||
$$\dfrac{A\omega}{\varepsilon_0}=\oint \overline{E} \overline{dA}=2EA$$ | $$\dfrac{A\omega}{\varepsilon_0}=\oint \overline{E} \overline{dA}=2EA$$ | ||
| 26. sor: | 29. sor: | ||
$$E=\dfrac{\omega}{2\varepsilon_0} $$ | $$E=\dfrac{\omega}{2\varepsilon_0} $$ | ||
| − | A kapott eredményt érdemes összevetni | + | A kapott eredményt érdemes összevetni az [[Elektrosztatika példák - Egyenletesen töltött korong tengelye mentén az elektromos tér|Egyenletesen töltött korong tengelye mentén az elektromos tér]] feladat $(R\longrightarrow \infty)$ határértékben kapott végeredményével. |
</wlatex> | </wlatex> | ||
A lap jelenlegi, 2013. szeptember 13., 09:56-kori változata
Feladat
- Végtelen kiterjedésű síkon
felületi töltéssűrűség van. Határozzuk meg a térerősséget a Gauss-tétel segítségével a síktól 
távolságra!
Megoldás
A Gauss-tétel alkalmazásához fel kell vennünk egy zárt felületet a térben. Ez legyen egy téglatest, melynek a töltött síkkal párhuzamos lapjai egyenként 
területűek. Az területű lapok a töltött sík átellenes oldalain helyezkednek el, attól egyaránt távolságra. (ábra) Az így definiált téglateste írjuk fel a Gauss-törvényt:
![\[\dfrac{Q}{\varepsilon_0}=\oint \overline{E} \overline{dA}\]](/images/math/d/e/7/de7487da9b625bb1aa418a39896332f4.png)
Ahol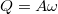 
a felvett téglatest által bezárt töltés mennyisége.
A rendszer szimmetriája miatt kijelenthetjük, hogy az elektromos tér mindenütt merőleges lesz a töltött síkra. Ebből következik, hogy a téglatest töltött síkra merőleges oldalfalain az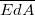 
skalárszorzat minden pontban azonosan nulla lesz, hiszen ezen felületek normálisa mindenütt 
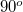-os szöget zár be a 
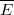térerősséggel.
A töltött síkkal párhuzamos felületű lapokon viszont a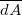 
felületnormális és a 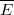térerősség minden pontban párhuzamos egymással, így azok skalárszorzata megegyezik a vektorok abszolút értékének szorzatával: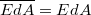 
A térerősség zárt felületre felvett integrálja az alábbi formára egyszerűsödik:
![\[\dfrac{A\omega}{\varepsilon_0}=\oint \overline{E} \overline{dA}=2EA\]](/images/math/c/f/1/cf1039c000c11e1f7191b54fee700ad6.png)
Ebből a térerősséget kifejezve:
![\[E=\dfrac{\omega}{2\varepsilon_0} \]](/images/math/e/2/6/e26be922b627f50e8d32ed593468c2e1.png)
A kapott eredményt érdemes összevetni az Egyenletesen töltött korong tengelye mentén az elektromos tér feladat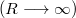 
határértékben kapott végeredményével.
